Matemàtiques a secundària. Competència digital
- guia
- Mòdul 0
- Mòdul 1
- Mòdul 2
- Mòdul 3
- Mòdul 4
- Mòdul 5
- Mòdul 6
- projecte
- índex
Fractals
A Fractals Unit for Elementary and Middle School Students. Unitat didàctica sobre fractals per a estudiants de primària i secundària
A Internet hi ha molta informació sobre fractals i eines per obtenir-ne representacions, en català i altres idiomes. Però en la nostra llengua es fa difícil trobar alguna web directament utilitzable a l’aula amb alumnes d’ESO.
Per això, en aquesta pràctica hem decidit treballar amb els continguts d’una web en anglès, didàcticament bona i de bon entendre malgrat l’idioma. Veureu com la introducció dels fractals motiva el treball amb perímetres, àrees, fraccions i potències d’una manera ben poc convencional i també convida a introduir qüestions d’història de les matemàtiques, sobre la investigació matemàtica i la utilitat pràctica de les matemàtiques.
Aquesta mateixa web pot servir d’introducció als fractals per a alumnes de batxillerat interessats a fer un treball de recerca sobre aquest tema.
Desenvolupament de la pràctica
La web que analitzareu es troba a l’adreça http://math.rice.edu/~lanius/frac/. L’autora és Cynthia Lanius. En aquesta pràctica, estudiareu el contingut de la web i veureu la manera d’aprofitar aquest material per programar unes classes d’ESO. Les lliçons que es presenten en aquesta pràctica s’han traduït més o menys literalment. Si voleu, podeu utilitzar eines de traducció en línia, com per exemple l’Altavista, per acabar de traduir les lliçons o paràgrafs de la web que més us agradin. De fet, això serà el que haureu de fer si trieu l’exercici 4 d’aquest mòdul.
0) Els continguts de la web
A la mateixa pàgina d’entrada trobareu, sota la portada, la introducció de la unitat didàctica i, a la columna de l’esquerra, amb el fons de color groc, podeu veure el menú de continguts que serveix també de mapa de la web. A la imatge següent teniu una traducció d’aquest menú.
1) Notes del mestre/a
Aquesta és la pàgina d’orientacions per al professorat: http://math.rice.edu/~lanius/frac/Tch_Notes/ A continuació, trobareu la traducció completa:
Aquestes lliçons, escrites seguint els Estàndards del NCTM, utilitzen la geometria fractal per introduir els alumnes en la recerca matemàtica moderna i reforçar les competències escolars en aritmètica i geometria.
2) Per què els fractals?
Aquesta és la primera lliçó sobre fractals: http://math.rice.edu/~lanius/fractals/WHY/, i us fem una traducció resumida a continuació:
- Són nous!
La major part de la geometria estudiada a secundària va ser organitzada per Euclides 300 anys abans de Crist. En canvi, els fractals es van descobrir al segle XX i són objecte d’investigació pels matemàtics actuals. - Els podem entendre:
A diferencia de molts temes de matemàtiques, per als quals fan falta anys d’estudi per poder-los entendre, hi ha molts aspectes dels fractals que els alumnes poden entendre. - Els objectes naturals sovint tenen estructura fractal:
Arbres, núvols, línies costaneres… són modelitzats i descrits molt millor pels fractals que no pas pels objectes geomètrics clàssics com triangles, quadrats… - Hi ha conceptes realment sorprenents relacionats amb els fractals:
Si mesureu la línia de la costa utilitzant mapes a una escala cada cop més reduïda, veureu que la mesura obtinguda va variant i cada cop és més gran… - Els científics utilitzen els fractals per resoldre problemes de la vida real.
Trobareu, també en aquesta pàgina, un seguit d’enllaços interessants per ampliar cada un dels motius per estudiar fractals, en anglès. Els alumnes han d’investigar seguint els enllaços per respondre aquestes preguntes:
- Qui va organitzar la geometria en una sèrie de llibres? Com s’anomenen aquests llibres?
- Escriu el nom d’un matemàtic o matemàtica que faci recerca actualment. On treballa? En quina àrea de les matemàtiques treballa?
- Troba una altra imatge d’un fractal que sembli un objecte natural.
Donat el seu caràcter, aquesta lliçó es podria treballar interdisciplinàriament amb l’àrea de llengua anglesa, o bé podríeu fer una recerca per Internet intentant trobar informació equivalent en català. Per exemple, els elements d’Euclides estan traduïts al català a Internet. Per aprofitar millor la classe, seria convenient fer la recerca pel vostre compte i presentar als alumnes les adreces que voleu que consultin. Algunes d’aquestes adreces catalanes les trobareu referenciades al final d’aquesta pràctica.
Cynthia Lanius proposa que els alumnes redactin les respostes en un processador de textos i les enviïn per correu electrònic.
3) Activitats sobre el floc de neu de Koch
En aquest apartat de la pràctica, teniu la traducció de les pàgines de Cyntia Lanius sobre el floc de neu de Koch. Són instruccions adreçades als alumnes per dirigir el seu treball a l’aula. Podeu copiar-les i enganxar-les editant-les convenientment en un processador de textos, imprimir-les i fer fotocòpies per fer aquestes activitats amb els vostres alumnes.
3.1) Dibuixar el floc de neu en paper engraellat
Imprimiu-vos el paper engraellat triangular per fer els dibuixos amb comoditat.
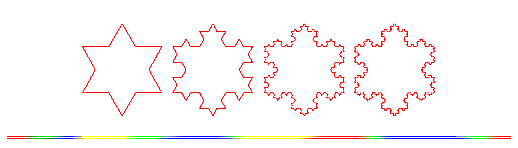
- Primer pas:
Comenceu dibuixant un gran triangle equilàter. - Segon pas:
Feu una estrella.- Dividiu un dels costats del polígon en tres parts iguals i esborreu la part del mig.
- Substituïu la part esborrada per dos segments d’igual longitud que el que heu esborrat formant un angle de 60 graus a la part exterior del polígon.
- Repetiu això mateix sobre cada un dels costats del polígon.
Repetiu el segon pas una i altra vegada. Feu-ho infinites vegades i tindreu el fractal.
3.2) Utilitzar un applet Java per veure el dibuix del floc de neu
Els alumnes poden veure les successives iteracions i comparar amb els seus dibuixos. El funcionament de l’applet és ben senzill i no necessita explicació. Aquí teniu una imatge i l’adreça web.
Des de d’aquesta adreça podey veure el funcionament de l’applet:
http://math.rice.edu/~lanius/frac/koch/koch.html
3.3) Un fenomen fascinant: perímetre infinit
El perímetre és una característica molt interessant del floc de neu de Koch. Normalment en augmentar el perímetre d’una figura geomètrica, també augmenta la seva àrea. Si teniu un quadrat amb un perímetre gran, la seva àrea també és gran. Però espereu a veure què passa aquí!
Recordeu el procediment per obtenir les successives figures:
- Dividiu un dels costats del polígon en tres parts iguals i esborreu la part del mig.
- Substituïu la part esborrada per dos segments d’igual longitud que el que heu esborrat formant un angle de 60 graus a la part exterior del polígon.
- Repetiu això mateix sobre cada un dels costats del polígon.
Investiguem el perímetre tot seguit.
Primera qüestió: si el perímetre del triangle equilàter inicial és de 9 unitats, quin és el perímetre de les tres figures següents? Expresseu el resultat en forma de fracció de 9. Indicació: (podeu dir-ho als alumnes o conduir-los perquè ho descobreixin ells mateixos) imagineu que la figura inicial té cada costat format per tres parts iguals i noteu que a la figura següent se substitueixen aquestes tres parts iguals per quatre parts iguals a les anteriors. Segona qüestió: veieu alguna pauta en la variació dels perímetres? El perímetre de cada figura és ___ vegades el perímetre de la figura anterior. Tercera qüestió: si el perímetre del triangle inicial és de 9 unitats, quantes iteracions calen per obtenir un perímetre de 100 unitats? (o tan proper a 100 com sigui possible). Utilitzeu la calculadora. Quarta qüestió: imagineu que repetiu el procés moltes i moltes vegades. El perímetre no para de créixer! Però també creix l’àrea?
Indicació per al professorat (podeu dir-ho als alumnes o conduir-los perquè ho descobreixin ells mateixos): l’àrea està tancada dins el cercle circumscrit al triangle inicial. Si seguíssiu el procés, permeteu-me dir-ho, infinites vegades, la figura tindria un perímetre infinit, però la seva àrea seria menor que l’àrea del cercle circumscrit.
Un perímetre infinit tanca una àrea finita. És fascinant!
3.4) I què passa amb l’àrea?
En el floc de neu de Koch un perímetre infinit tanca una àrea finita. El perímetre del floc és més gran a cada iteració. Però què passa amb l’àrea? Imagineu que dibuixeu un cercle que contingui la figura inicial. No importa quant gran sigui el perímetre, l’àrea de la figura es manté dintre el cercle. Podem calcular l’àrea de la figura?
Dibuixeu unes quantes iteracions utilitzant paper triangulat i investigueu com va creixent l’àrea. Recordeu el procediment seguit per passar d’una figura a la següent.
Observeu a la imatge anterior la segona iteració del floc de neu de Koch. Observeu que el triangle inicial (de color groc) està contingut dins el floc de neu de Koch amb tres triangles menors (de color vermell) afegits a la primera iteració, i dotze triangles encara menors (de color blau) afegits en la segona iteració. Així que trobar l’àrea del floc de neu de Koch és un problema de sumar. Trobeu l’àrea del triangle inicial, sumeu-hi l’àrea dels triangles vermells per a la primera iteració i sumeu els dotze triangles blaus per a la segona iteració.
Podeu fer servir els triangles de la graella triangular per mesurar l’àrea. El triangle original de color groc conté 81 triangles petits. Quina és l’àrea de cada triangle vermell i de cada triangle blau? Organitzeu les dades en una taula.
| Iteració | Àrea de cada triangle afegit | Número de triangles afegits | Àrea total afegida | Àrea total de la figura |
| – | 81 | |||
| 1 | 9 | 3 | 27 | 108 |
| 2 | 1 | 12 | 12 | 120 |
Observeu què està passant. L’àrea del floc de neu no para de créixer però ho fa cada cop més lentament. Està convergint cap a algun número, acostant-s’hi més i més, però mai hi arribarà de manera exacta.
Programació de l’activitat
Requeriments de maquinari i de programari: Per dur a terme l’activitat necessiteu un ordinador connectat a Internet per a cada dos o tres alumnes, un navegador d’Internet amb Java activat, un processador de textos i un full de càlcul. Metodologia: Per fer les activitats d’aquesta unitat didàctica es pot combinar el treball a l’aula d’informàtica amb el treball amb paper i llapis. Traduïu les lliçons que voleu treballar i elaboreu-ne, per cada una, un document imprimible amb instruccions breus i suficients per provocar la recerca, la reflexió i la descoberta per part dels alumnes. És recomanable el treball en grup per discutir conceptes i per elaborar les conclusions de cada lliçó. Material per a l’alumnat: Fotocòpies amb instruccions breus i adreces d’Internet concretes per a cada sessió de treball. Fotocòpies de l’engraellat triangular. Paper i llapis per als resums i càlculs dels alumnes. Avaluació: En acabar cada lliçó els alumnes hauran de lliurar, per grups, el document de treball, que serà un element avaluador bàsic, juntament amb les actituds demostrades per cada alumne/a durant les sessions. Temporització: És bastant difícil definir una temporització exacta. Caldrà estar ben atents a les característiques del grup i dinamitzar el ritme quan convingui. Cada lliçó es pot completar en una o dues hores de classe i, si es proposa de fer un petit treball sobre allò que s’ha après, farà falta encara una altra hora de classe per posar els resultats en comú.
Informació complementària
Aquí teniu un recull d’adreces sobre fractals que poden ser d’utilitat per fer un treball de recerca a batxillerat. Només es relacionen aquelles adreces en idioma català o castellà:
- Títol: Área fractal
Autor: Sysifus
Idioma: castellà
Indicació: informació molt bona i imatges estàtiques i animades de fractals
Adreça web: http://www.arrakis.es/~sysifus/index.html - Títol: Fractales.org
Autor: Jl Andrés
Idioma: castellà
Indicació: articles sobre fractals, caos i ciència
Adreça web: http://www.fractales.org/index.php - Titol: Objetos fractales
Idioma: castellà
Indicació: introducció als fractals per a treballs de recerca de batxillerat
Adreça web: portal edu365.cat - secció “com soc”
Miniaplicacions de tot tipus per generar fractals de diverses menes:
- Generador d’arbres fractals a la web de Jaume Bartrolí:
http://www.xtec.cat/~jbartrol/fractals/ptgen.html - El joc de la vida i altres fractals en applets a la web de virtual manipulatives
Conway game of life - Pascals triangle - Koch and Sierpinski - Mandelbrot and Julia Sets - i altres fractals generats interactivament. - Iteracions: atractors fractals en un projecte de JR Arduny, fet amb la calculadora Wiris.
- El joc del caos i el triangle de Sierpinski de Teresa Cortada, projecte fet amb la calculadora Wiris.