Matemàtiques a secundària. Competència digital

A la guia del curs, hi podeu llegir:

”…els alumnes del curs només haureu de fer 3 pràctiques i lliurar 3 exercicis atenent a l’especialització que tingueu cadascun de vosaltres, si és el cas. Per exemple, a un professor/a especialitzat en 1r. cicle d’ESO se li aconsella que faci les pràctiques i exercicis 1), 2) i 4), a un professor especialitzat en batxillerat, les pràctiques i exercicis 2), 3) i 4)… etc. Qualsevol altra combinació d’aquests 4 elements agafats de 3 en 3 serà acceptada…”

Ja teniu l’aparició de la combinatòria. Hi intervenen tots els elements? Importa l’ordre? Es poden repetir els elements? Si sabeu respondre aquestes qüestions i teniu clara la teoria, podreu saber si es tracta de variacions, permutacions o combinacions. Doncs, d’això, de combinatòria, és del que tracta aquesta pràctica.

Aquesta pràctica és adient per al professorat de 2n cicle d’ESO.

A partir del web de la XTEC podeu enllaçar amb l’activitat d’aquesta pràctica seguint la ruta XTEC | Escola Oberta | Matemàtiques, i veureu l’enllaç al web següent.

L’autora és Carme Flavià. L’espai web compta amb un seguit d’explicacions teòriques i d’exemples i exercicis. Convé remarcar que l’activitat també disposa d’una activitat d’autoavaluació.

Entreu a l’enllaç del material que treballareu http://phobos.xtec.cat/iesnarcisoller/intranet/departaments/mates/combi/index.htm

1) Variacions ordinàries 1.1 ) Exposició

En el primer dels enllaços, l’autora dóna la definició següent: “diem variacions ordinàries de m elements diferents, agafats de n en n, als grups que es poden formar de n elements diferents amb els m, de manera que dos grups siguin diferents tant si tenen algun element diferent o aquests estan col·locats en ordre diferent”.

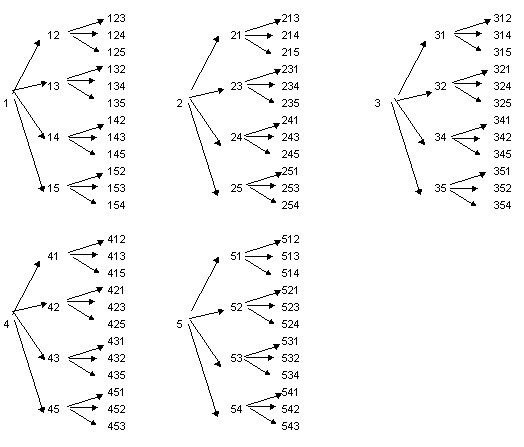
Exemple 1: Voleu saber quants i quins grups de tres elements diferents es poden formar amb els números: {1, 2, 3, 4, 5 }.

Es mostra l’arbre següent:

}

En aquest diagrama veiem que, de cada un dels 5 elements originals, surten 4 fletxes i, de cada una d’aquestes 3. Per saber el número de grups de tres elements diferents que es poden formar amb els 5 elements originals, haureu de multiplicar: 5·4·3.

En general, la fórmula per trobar el número de variacions ordinàries és:

V m,n=m·(m-1)·(m-2)·(m-3)· … ·(m-n+1)

Exemple 2: Us interessa saber quantes i quines banderes tricolors es poden formar amb els colors: { blau, verd, rosa, negre }.

Per saber quantes banderes són s’utilitza la fórmula anterior: V4,3 = 4·3·2 = 24 I si cal, es pot visualitzar l’arbre següent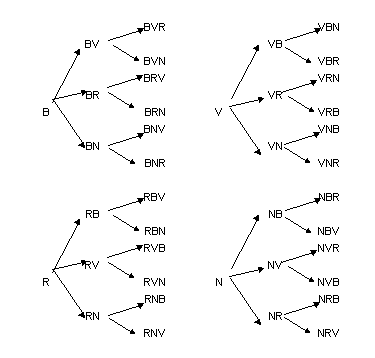

1.2) Exercicis

Aquest primer apartat sobre les variacions s’acaba amb l’enllaç als exercicis sobre variacions ordinàries:

Seguiu l’enllaç i resoleu els 10 problemes plantejats. 1.3) Solucions

Fixeu-vos que també hi ha l’enllaç a les solucions als 10 problemes plantejats.

2) Apartats sobre variacions amb repetició, permutacions ordinàries, permutacions amb repetició i combinacions ordinàries

Els altres enllaços dels apartats posteriors

repeteixen sempre el mateix esquema:

• exposició de l’apartat
• alguns exemples resolts amb arbre
• fórmules que cal recordar
• i enllaços als problemes amb les solucions.

3) Problemes

A la pàgina principal, a la part inferior esquerra, hi trobeu un enllaç anomenat problemes, en aquesta pàgina hi veureu un recull de 10 problemes. Aquí caldrà distingir quin dels casos anteriors es tracta. Per aquest motiu, hi ha enllaçada la imatge següent amb un quadre-resum per identificar de quin tipus d’exercici es tracta:

Cal destacar que també hi ha les solucions dels 10 problemes plantejats.

4) Autoavaluació

També a la part inferior esquerra de la pàgina principal, hi trobeu un enllaç anomenat autoavaluació. En aquesta pàgina hi ha el formulari següent:

Convé destacar que el botó Enviar tramet la resposta del formulari per correu electrònic a l’autora del treball. El vostre navegador obrirà el programa gestor de correu per defecte, i des d’ell, els vostres alumnes podran enviar les respostes del formulari a l’adreça que vosaltres indiqueu.

• Requeriments de maquinari i de programari: Necessitareu un ordinador per a cada un o dos alumnes, amb connexió a Internet.
• Metodologia: Convé que l’activitat tingui una motivació inicial basada en algun problema de la vida real. Els esquemes en arbre ajuden molt a estructurar la informació rebuda en un problema, per tant, caldrà que els alumnes els dibuixin amb cura. Es pot anar a l’aula d’informàtica amb el treball una mica preparat amb els exemples motivadors. Explicareu en línies generals el funcionament de la unitat als alumnes. Si disposeu de projector a l’aula, podeu fer-lo servir per a aquesta explicació.
  Passareu d’ordinador en ordinador per resoldre dubtes, comprovar com van progressant. Si detectem que un enunciat té alguna dificultat especial, farem una explicació per a tota la classe aprofitant el projector o la pissarra, si és el cas.
  Un cop fetes les activitats, faran l’Autoavaluació, aquesta es pot enviar per corrreu electrònic o, havent-la imprès abans, fer-ne còpies en paper i recollir-la. També es pot dissenyar una altra prova d’avaluació diferent.
• Material per a l’alumnat: Els alumnes hauran de dibuixar esquemes en forma d’arbre, fer alguns càlculs auxiliars i una prova escrita, per tant, hauran de portar estris d’escriptura.
• Temporització: Es pot estimar en tres sessions classe el temps necessari per dur a terme tota aquesta proposta, i tal vegada una sessió més per a l’avaluació.

Altres enllaços amb recursos sobre combinatòria

• Títol: Combinatoria
  Autor: Adolfo Cid Valle
  Idioma: espanyol
  Adreça web: http://thales.cica.es./rd/Recursos/rd99/ed99-0516-02/ed99-0516-02.html