|
|
||||||||||||||||
 |
||||||||||||||||
 |
Pràctica |
 |
 |
 |
 |
 |
|
|
Exercicis
|
 |
||||||
|
|
Geometria constructiva versus geometria analítica |
|
|
|
| És clar que sempre que fem geometria amb la Wiris (o amb el Cabri, la Cinderella...), al darrere hi ha la geometria analítica. La pantalla de treball de la Wiris ens permet visualitzar les equacions, però, alhora, ens obliga a un procés constructiu i ens permet posar l'èmfasi més en el problema que no en les eines per resoldre'l. D'aquesta manera, desapareix el fals dilema geometria constructiva o geometria analítica i se li dóna l'única resposta interessant: geometria. | |
|
En aquesta pràctica veurem com la Wiris integra els
dos mètodes de treball habituals en la geometria: el mètode
constructiu i el mètode analític. Farem un resum de les
comandes aplicables als triangles, entre d'altres, necessàries
per desenvolupar aquesta aplicació didàctica: la construcció
i visualització de la recta d'Euler d'un triangle interactiu. En
|
|
|
Dos blocs d'instruccions diferents per resoldre el mateix problema |
|
En la pràctica 6 del mòdul 1 vam veure el problema de trobar el quart vèrtex D d'un paral·lelogram, donats tres vèrtex A, B i C. Tot i que es començava exposant un mètode vectorial, ja es va comentar que no era la única manera de resoldre el problema. Ara podeu recordar les dues maneres: podeu fer clic a la icona de l'esquerra per veure i executar els dos blocs de comandes en una finestra activa de la Wiris. |
 |
|
La imatge anterior no requereix més explicacions.
Només hi falten les ordres per dibuixar el tauler gràfic.
Recordeu que trobareu les icones per entrar les comandes punt,
recta, paral·lela...
a la carpeta 
i la icona  la trobareu
a la carpeta 
i que l'assignació 
serveix perquè el tauler gràfic de la Wiris s'actualitzi interactivament
en moure els punts inicials A, B i C. Pel que fa a
la intersecció de figures i la necessitat de considerar sempre el
resultat d'una intersecció un conjunt o llista, heu de saber que
aquest tema es tracta a fons en la pràctica
6. |
|
|
|
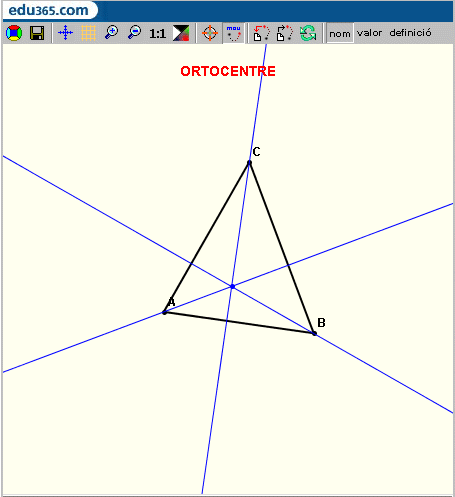
Punts notables d'un triangle: exemple de l'ortocentre |
|
|
|
|
|
|
|
Dels quatre punts notables d'un triangle que s'estudien a la secundària (ortocentre, baricentre, incentre i circumcentre), tres estan alineats. La recta que els conté s'anomena recta d'Euler. En l'exercici 2 d'aquest mòdul se us demana que construïu una pantalla activa de la Wiris per mostrar interactivament els quatre punts notables d'un triangle i la recta d'Euler. En la pantalla activa de l'esquerra trobareu l'exemple que dóna lloc a la imatge anterior amb diferents maneres de construir l'ortocentre utilitzant els recursos que incorpora la Wiris. Al final d'aquesta pàgina trobareu més recursos de la Wiris relacionats amb segments i triangles, que us resultaran d'utilitat per fer l'exercici 2. A continuació, es detallen les comandes emprades en la finestra activa de l'esquerra. |
| Comencem definint i dibuixant un triangle i els seus vèrtexs: | |
 |
|
|
|
|
| Podem trobar l'ortocentre definint les rectes que contenen les altures i resolent el sistema donat per les seves equacions. Recordeu que el resultat de resoldre un sistema és una llista de taules, en aquest cas, la llista té un únic element, que és la taula {x = a, y = b}. Recordeu la sintaxi per recuperar el punt solució del sistema en la imatge següent. Si voleu repassar els conceptes de llista i de taula, podeu consultar la pràctica 1 del mòdul 2. | |
 |
|
|
Finalment, establim les propietats del tauler gràfic i dibuixem els elements que falten: les altures i el títol de l'activitat. |
|
 |
|
| Però la Wiris té recursos que ens estalvien molta feina, com les comandes altura i ortocentre. Vegeu-ne la sintaxi: | |
 |
|
 |
|
|
|
|
|
|
Més comandes de la Wiris relacionades amb triangles i polígons |
Tal com ja hem vist
i utilitzat anteriorment, la comanda segment,
icona  de
la carpeta ,
serveix per construir segments. Accepta com a arguments els dos punts extrems
o bé un punt i un vector. Algunes funcions aplicables als segments
són longitud i punt_mitjà.
Aquesta darrera comanda es pot aplicar directament a una parella de punts. |
|
Altres comandes relacionades amb els
triangles són mitjana, bisectriu,
baricentre, circumcentre,
incentre, circumradi
i inradi. Totes elles reben com a argument un
triangle, que pot estar donat per un identificador, i retornen el que el
seu nom indica. La comanda bisectriu es pot introduir amb la icona 
de la carpeta .
La sintaxi d'aquestes comandes és semblant a la que heu vist en la
finestra activa anterior, amb l'exemple de l'altura
i l'ortocentre. |
|
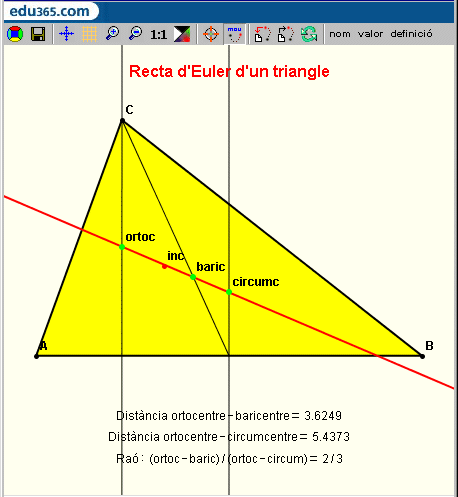
| En l'exercici 2 d'aquest mòdul se us proposa construir un tauler gràfic semblant al de la imatge amb un triangle interactiu que mostri l'ortocentre, el baricentre, l'incentre, el circumcentre i la recta d'Euler del triangle. Opcionalment, podeu fer que aquest tauler també mostri visualment per què el baricentre està dintre el segment determinat pels altres dos punts de la recta d'Euler amb raó de distàncies 2/3. | |
|
|
|
El baricentre es troba entre l'ortocentre i el circumcentre, amb raó de distàncies 2:3 |
|
|
|
Com incorporar gràfics de la Wiris a un document PDF per imprimir amb alta qualitat |
| Heu de saber que la Wiris permet incorporar gràfics a un document PDF amb la qualitat PDF, molt més acurada que la resolució de pantalla. Podem apreciar aquesta qualitat si disposem d'una impressora adequada. Això vol dir que amb la Wiris podem produir documents impresos amb gràfics geomètrics d'alta qualitat. El procediment que s'ha de seguir és aquest: | |
|
|
|
Podeu veure una animació que fa visual
aquest procediment, clicant a la icona de l'esquerra. Aquí teniu el document text.pdf resultant amb el dibuix anterior i un comentari escrit en Word. |
 |
|
|
|
