DPMA. Mòdul 3. Pràctica 4. Internet i les matemàtiques


	Entenguem les sumes de fraccions

	L'objectiu d'aquesta pràctica és conèixer i entendre un dels aspectes que més costen d'assimilar i que són la base de l'àlgebra matemàtica: les fraccions. Per fer el procés complert, treballareu diferents àmbits de l'aprenentatge: l'explicació, l'estudi i la sistematització. De fet, aquest és el procés que sempre heu de tenir present en la introducció dels nous conceptes. Durant l'explicació, no podeu fer solament una lliçó magistral, heu de mostrar exemples comprensius i pràctics d'allò que voleu explicar i us ajudeu d'algunes activitats que hi ha a la xarxa. Activitats que simulen situacions que, d'altra banda, costarien molt de fer a la classe. L'alumnat ha de redescobrir allò que se li ha explicat on hi ha exemples a la xarxa. Per acabar, cal sistematitzar allò après, els exercicis, i d'aquests també en teniu, i molts, a Internet. Tot i així, es recomana fer experiències amb materials reals com omplir una o més ampolles amb aigua dividides prèviament amb parts, posar l'aigua a una altra, retallar o plegar un full en parts iguals..., activitats que ajuden a introduir el concepte de fraccions. Un cop el nen o la nena té clar el concepte de les parts, caldrà avançar cap a la interrelació entre elles: les operacions (la suma, la resta, la divisió i el producte). La pràctica se centra en la suma, però podeu practicar amb les altres operacions.

	Desenvolupament de la pràctica

	Es dividideix la pràctica en tres parts : Activitats que serviran d'ajut al mestre/a per explicar i que poden ser utilitzades mitjançant les pissarres digitals. Activitats d'aprenentatge on els alumnes descobreixen. Activitats de sistematització on les assimilen.

	Primer punt per desenvolupar: l'explicació

	Aneu a la pàgina http://www.schoolhousetech.com/products/download.htm. Necessiteu un projector a la classe o a l'aula d'informàtica per fer l'explicació del concepte. El primer que fareu és recordar què és una fracció. Aneu a l'adreça: Fraccionador i us surt la pàgina següent: Cerqueu un nombre per al numerador i un altre per al denominador, d'aquesta manera, creareu una fracció. A continuació, podeu veure la fracció mitjançant les parts del cercle o el rectangle. Cal recordar que les parts pintades formen el denominador i les parts totals (les pintades més les altres) el numerador. Un cop recordat i treballades les parts, aneu a operar amb elles. Per poder seguir explicant el concepte, aneu a l'adreça: http://www.jverdaguer.org/mestres/pares/sise/fraccions/partspera6.swf i podreu fer l'explicació en grup gran. També podeu explicar com es divideix la unitat en parts iguals tot treballant el concepte de denominador a l'adreça: http://www.xtec.net/recursos/mates/aqui/fraccions/fraccions.htm i el treball de les parts d'un nombre a la següent: http://www.jverdaguer.org/mestres/pares/sise/mulidiv/partsnombre.swf. Un cop recordat i treballades les parts, opereu amb elles. Expliqueu què vol dir sumar fraccions, més que fer-ne. Per explicar-ho d'una manera comprensiva, aneu a la pàgina http://www.jverdaguer.org/mestres/pares/sise/setembre04/fraccentendre.swf i mireu l'animació. Després, mireu una altra activitat que ajuda a entendre la suma a la pàgina següent: http://www.jverdaguer.org/mestres/pares/sise/setembre04/sumfra6.swf. Mentre mostreu l'animació, podeu anar fent preguntes com: En quantes parts està dividit el primer cercle, en quantes el segon? Quantes parts estan pintades a cada un? Estan dividits amb la mateixes parts? A les divisions, com es diuen divident o divisor? El divisor on es col·loca en una fracció? ...
	Cal anar remarcant que, per poder sumar dues fraccions, cal primer que les dues tinguin el mateix denominador, és a dir, que estiguin dividides en parts iguals. Per dividir en parts iguals, cal tenir clar el concepte de fraccions equivalents. Per reforçar aquest concepte, aneu a l'activitat següent: http://www.jverdaguer.org/mestres/pares/sise/setembre04/fraccionsequi.swf i també aquesta altra activitat: http://www.jverdaguer.org/mestres/pares/sise/setembre04/fraccionsequi2.swf la podeu proposar als alumnes per reforçar el tema abans de fer les sumes i les multiplicacions. Fixeu-vos que són dues activitats diferents però complementàries. A l'explicació amb presentacions visuals cal afegir sempre activitats manipulatives que complementin i facin tangible la comprensió del que voleu transmentre. En aquesta primera pràctica heu intentat explicar el lligam que hi ha entre la suma de fraccions i els conceptes previs que es necessiten per arribar a resoldre les diferents operacions.
	Segon punt per desenvolupar: l'estudi
	Un cop presentada l'activitat, cal que els alumnes la descobreixin per si mateixos ja que és l'única manera que construiran el seu coneixement. Per fer-ho, poden reutilitzar les mateixes eines que ha fet servir el mestre/a. La més útil i en la qual poden veure si ho estan aprenent o encara han d'investigar més és la segona: http://www.jverdaguer.org/mestres/pares/sise/setembre04/sumfra6.swf. L'activitat consta de dues parts: la primera, l'estudi (que el mestre/a ha de presentar) i la segona, la pràctica. Els alumnes se centraran, primer de tot, en l'estudi perquè puguin preguntar allò que no han acabat d'entendre. També a la pàgina de l'Enciclopèdia Britànica http://britannica.edu365.com/browse/learning?topic=k5_math_manipulatives_numbers trobareu activitats relacionades amb les fraccions. Practiqueu una estona amb totes elles. Mireu un exemple a la imatge de sota:

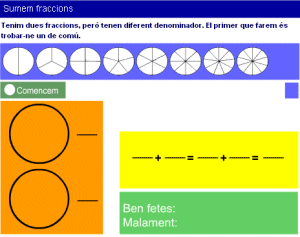
	Exemple de l'activitat

	Tercer punt per desenvolupar: la sistematització del concepte

	Ara dueu a terme activitats que reforcin els conceptes apresos per arribar a entendre i assimilar la suma de fraccions: Dividir un objecte en parts Trobar fraccions equivalents Sumar fraccions Com que el que esteu treballant és la comprensió, i no exactament la mecànica de la suma, podeu dedicar-hi ben bé dues sessions a fer exercicis, ja que aquests són de raonament i no de "matxaca".
	Per fer-ho agafeu l'exercici que heu anat treballant http://www.jverdaguer.org/mestres/pares/sise/setembre04/sumfra6.swf però ara trieu l'opció Per resoldre tot sol i us apareixerà la pàgina següent:

	Sempre, per començar una activitat heu de prémer Comencem. Apareixen els dos cercles dividits en parts aleatòries cada un i al seu costat la fracció que representa. Amb els cercles de la part superior: Heu de dividir els dos cercles en les mateixes parts. Un cop trobat, veureu que surt el denominador comú. Cal fer molt d'èmfasi en aquest pas. Arribat aquest punt, cal utilitzar, ara sí, la mecànica de la suma de fraccions: se'ls pot donar un document adjunt "xuleta", ja que això només és la part mecànica.
	Programació de l'activitat

	La metodologia s'ha explicat en el desenvolupament de l'activitat. Pel que fa al treball sistemàtic, es pot treballar de dos en dos, tot i que recomanem fer-ho a tall individual, ja que és un concepte que s'ha d'interioritzar. No obstant, si el grup discuteix i comenta el tema també és positiu. Objectius curriculars: Treball de les parts d'un objecte o d'un nombre. Treballeu la suma de fraccions. Objectius TIC: El domini del joc a través del ratolí. La navegació per trobar els exercicis. Es pot dir que la instal·lació de plug-in (del Flash) per executar-los. Temps: cal dedicar-hi temps a aquest tema. Tot i que aquesta activitat està emmarcada al cicle superior, cal haver treballat, en cursos anteriors, les parts (ja des de primer de primària amb 1/2, 1/3) i tenir clar tot el claustre d'utilitzar una metodologia comuna donant importància a la comprensió. Material: cal disposar de molts mitjans manipulatius, com l'ordinador, pissarra digital (si pot ser a l'aula), tisores, papers....


	El tema de les fraccions és un cavall de batalla a primària. Però en moltes ocasions no és culpa de l'alumne/a, sinó del fet de no disposar d'activitats adients, o bé de no saber prioritzar la comprensió i anar directament a la mecànica. Cal que les matemàtiques siguin sempre reflexives, comprensives i que es vegi una utilitat real. Les matemàtiques formen part del nostre món i només d'aquesta manera les podem fer nostres. Per això, cal perdre més temps en els procediments que en la mecànica. D'altra banda, ho faríem malament.

	Informació complementària

	Podeu cercar adreces d'Internet que treballen la simulació de fraccions encabides en altres contexts.