|
|
||||||||||||||||
 |
||||||||||||||||
 |
Pràctica |
 |
 |
 |
 |
 |
 |
Exercicis
|
 |
|||||||
Mostra d'unitats didàctiques
 |
||||||||||||||||
|
Unitats de mesura |
|
| Les mesures han estat introduïdes en la pràctica 2 del mòdul 1, on hem vist com s'escriuen les quantitats amb unitats a la Wiris i també com la Wiris pot calcular amb les mesures i les pot canviar d'unitats amb la comanda convertir. Recordem que una mesura és una quantitat representada mitjançant un nombre i una unitat. En aquesta pràctica veurem una petita col·lecció de problemes de mesures amb canvis d'unitats, de nivell de primer cicle de secundària, amb l'objectiu d'aprofundir una mica més en el tractament que fa la Wiris de les mesures i les unitats, focalitzant en les unitats de volum i capacitat les unitats angulars i les unitats de temps. | |
|
|
|
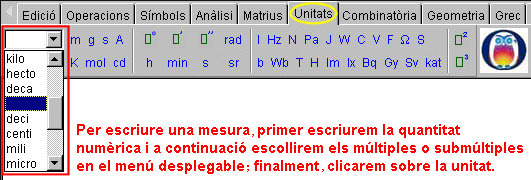
Unitats de la barra d'eines de la Wiris |
|
|
Si voleu conèixer el detall de totes les unitats del sistema internacional i d'altres que apareixen a la barra d'eines de la Wiris, podeu fer clic a la icona d'ampliació. |
|
Comandes per treballar amb mesures i unitats |
| La comanda convertir permet obtenir la mesura equivalent amb diferents unitats. Usualment, aquesta comanda tindrà dos arguments: el primerar serà la mesura (quantitat amb unitat) i el segon serà la nova unitat. Si volem obtenir la mesura equivalent amb unitats del sistema internacional no cal escriure el segon argument. | |
 |
|
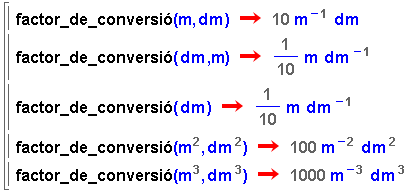
| La comanda factor_de_conversió dóna el factor pel qual cal multiplicar una mesura expressada en la primera unitat per obtenir la mesura equivalent en la segona unitat. Els arguments d'aquesta comanda són les unitats per aquest ordre. Si la segona unitat és del sistema internacional, només cal entrar un argument. | |
 |
|
| La comanda coeficient aplicada a una mesura (quantitat amb unitats) dóna com a resposta la quantitat numèrica, sense les unitats. Aquesta comanda és d'utilitat en algunes situacions, com quan volem comprovar un resultat o quan volem expressar una mesura amb les unitats escrites de diferent manera a com la Wiris ho fa, per exemple en el tauler gràfic. | |
 |
|
| La comanda unitat aplicada a una mesura ens retorna la unitat en què ve expressada aquesta mesura. | |
 |
|
|
|
Problemes de càlcul de volums de primer cicle d'ESO |
 |
Abans de proposar-vos una llista d'exercicis guiats, convé que us adoneu d'unes precisions que cal fer sobre el treball amb unitats i algunes possibilitats que teniu. Podeu engegar, si us sembla convenient, la calculadora Wiris i fer proves semblants a les que es proposen a la imatge següent. |
 |
|
|
Vegem com treballa la Wiris |
|
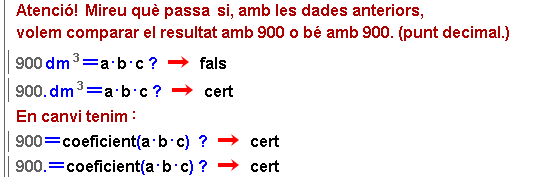
| Abans de proposar problemes a les vostres alumnes i els vostres alumnes, encara insistirem en el fet que la manera "natural" de treballar amb unitats, per a la Wiris, és fer servir nombres decimals. Vegeu-ho en la imatge següent: | |
 |
|
|
Convé que es facin servir decimals per a indicar resultats de càlculs amb unitats |
|
| Tot seguit teniu una col·lecció d'exemples senzills per remarcar petits detalls en la forma de treballar les unitats amb la Wiris i per constatar, també, el profit pedagògic que en podem treure, en forma de petits problemes guiats per ajudar els alumnes a assolir les habilitats més elementals en el tractament de les mesures. | |
 |
|
|
|
|
|
Cliqueu a la icona de l'esquerra per veure la
llista anunciada de problemes guiats, en una finestra activa de la Wiris,
sobre unitats de volum i capacitat, per a alumnes de primer cicle d'ESO.
Feu proves i avalueu el valor didàctic d'aquests exemples. Si voleu,
podeu adaptar per la Wiris una altra llista de problemes semblants. Recordeu
que per demanar l'entrada de dades des de la finestra activa de la Wiris
(caselles de color verd), utilitzem la icona Argument, ,
de la carpeta  .
|
| La Wiris també treballa amb expressions incomplexes de les mesures, separant les diferents unitats per un espai. Vegem en l'exemple següent com podem aprofitar-ho didàcticament: | |
 |
|
|
Expressions complexes i incomplexes de les mesures amb la Wiris |
|
|
|
En la finestra activa de l'esquerra trobareu la proposta anterior per treballar amb la Wiris les expressions complexes i incomplexes de les mesures de volum. Valoreu-ne la utilitat didàctica per a primer cicle d'ESO i escriviu a la mateixa finestra activa exercicis anàlegs per a les mesures de longitud i superfície. |
|
|
Mesures de temps. Treball amb la Wiris |
En l'exemple següent es proposen exercicis
senzills de conversions i operacions amb hores, minuts i segons. S'espera
que els alumnes facin els càlculs mentalment o a mà, i que
comprovin el resultat prement la icona 
de la finestra activa. També podeu utilitzar una mica de programació
per avaluar de manera automàtica una llista d'exercicis semblants,
identificant cada pregunta amb una variable, tal com es va explicar en la
pràctica 2 del mòdul 2. |
|
 |
|
|
Treball amb hores, minuts i segons |
|
|
|
Podem utilitzar la Wiris per proposar als alumnes exercicis pràctics de mesures de temps amb resposta automàtica. Cliqueu a la icona de l'esquerra per executar l'exemple anterior en una finestra activa. Escriviu i executeu exercicis semblants amb mesures angulars de graus, minuts i segons, en la mateixa finestra activa. |
|
Mesures angulars. Treball aritmètic i geomètric amb la Wiris |
|
|
|
|
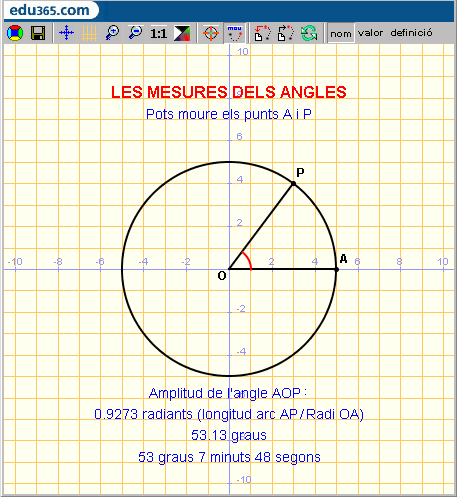
En el currículum actual tenim el sistema sexagesimal a primer cicle d'ESO i els radiants a segon cicle d'ESO i batxillerat. Les mesures angulars es poden treballar també geomètricament. Per defecte, la Wiris dóna els angles en radiants i cal fer la conversió per obtenir-los en el sistema sexagessimal. Cliqueu a la icona de l'esquerra per veure en funcionament el següent exemple didàctic per treballar interactivament les mesures angulars i les seves equivalències. A continuació, trobareu una explicació de les comandes emprades en aquest exemple. |
| Comencem definint els elements estructurals del dibuix i l'amplitud de l'angle AOP. A1 i B1 són punts auxiliars, que no dibuixarem, però que són necessàris per utilitzar la comanda punt_més_proper perquè el punt A es mogui sobre la recta y = 0 i el punt P sobre la circumferència T. Observeu la sintaxi de la comanda arc: el primer argument és el centre, el segon i en tercer són els dos punts de la circumferència inicial que definiran l'amplitud de l'arc (l'arc s'orienta segons l'ordre d'aquests dos punts) i el quart argument és el radi que volem que tingui l'arc. Convé destacar que per definir l'amplitud de l'angle utilitzem la comanda angle_orientat(A,O,P), en lloc de angle(A,O,P), perquè aquesta última dóna únicament amplituds entre 0º i 180º i aquí ens interessa obtenir els valors entre 0º i 360º, segons l'orientació de l'obertura entre OA i OB: | |
 |
|
| La variable an guarda el número de radiants de l'angle AOP. Ara passem a la varible angraus el número de graus (expressat en decimals) de l'angle AOP. La part entera de angraus serà el nombre de graus enters, que guardem a la variable grs. La part decimal la passarem a segons multiplicant per 3.600, i arrodonint el resultat a la part entera. Amb aquest número enter de segons, obtindrem els minuts i els segons com a quocient i residu de la divisió entera per 60. Finalment, grs, mins i segs són les variables que contenen l'expressió de l'angle en el sistema sexagessimal. | |
 |
|
| Finalment, les instruccions per dibuixar els elments i escriure les mesures calculades. Observeu com s'escriu el punt O perquè no es pugui moure. Observeu com es defineix el conjunt d'atributs del text i del títol. Això permet escriure els atributs una sola vegada i, per tant, unificar el format del text i fer-hi modificacions de forma ràpida: | |
 |
|
 |
|
|
|