|
|
Estadística |
| |
|
|
|
L'objectiu d'aquesta pràctica és conèixer les possibilitats
de la Wiris en el camp del treball estadístic.
Heu de saber que la manera d'entrar les dades i el fet de no poder-les
importar d'un altre entorn fan que no es pugui qualificar la Wiris com
un programari estadístic. Ara bé, en aquesta pràctica
i la següent podreu comprovar que, en canvi, té una gran potencialitat
com a eina didàctica, és a dir, com a ajuda en la presentació
dels conceptes.
|
| |
|
| |
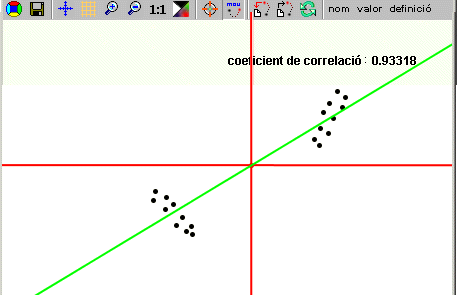
Una activitat didàctica amb la Wiris per interpretar
el coeficient de correlació.
Realment les 20 dades de la figura estan molt relacionades?
|
| |
|
|
|
La manera de manipular dades estadístiques
amb la Wiris |
| |
|
|
|
Els conjunts de dades a què la Wiris aplicarà les comandes
estadístiques es poden presentar, fonamentalment, de dues maneres:
- Com a llistes de nombres.
- Com un divisor, que és un objecte especial de la Wiris
que, ja que estem en l'àmbit de l'estadística, la manera
més fàcil d'entendre què representa és dir
que és una col·lecció de dades presentades en forma
de dada-freqüència.
Vegeu l'exemple següent de conjunts de dades presentats de les dues
maneres. Passem de l'una a l'altra amb la comanda compta_element,
que ja vam fer servir en el mòdul 4, o amb llista,
de què vam veure exemples semblants en el mòdul 2.

Vegeu la sintaxi per escriure els divisors, tancats amb [...]
i separant cada dada de la seva respectiva freqüència mitjançant
la icona  que teniu al menú que s'obre amb la pestanya
que teniu al menú que s'obre amb la pestanya  . .
Teniu una finestra activa auxiliar on podeu fer algunes pràctiques
i veureu la possibilitat de càlcul de paràmetres estadístics.
Adoneu-vos de la manera d'obtenir la freqüència d'una dada
i del fet que, tal com ja hem dit més amunt, el conjunt de dades
es pot entrar tant com una llista com en forma de divisor. Estudiem també
la comanda suport que ens dóna el conjunt
de valors observats sense tenir en compte la freqüència.
|
| |
|
|
|
Interpretació de la mitjana com a centre
de gravetat |
| |
|
| |
Tot seguit es presenta una activitat didàctica
que permet fer visual la idea fonamental de la mitjana com a element de
ponderació o centre de gravetat del conjunt de dades que s'estudia. |
| |
|
| |
Us suggerim que primer de tot feu l'exercici,
que podeu engegar amb la icona de Finestra activa (veureu que està
gravada de manera que el tauler gràfic s'obri automàticament). |
| |
|
|
|
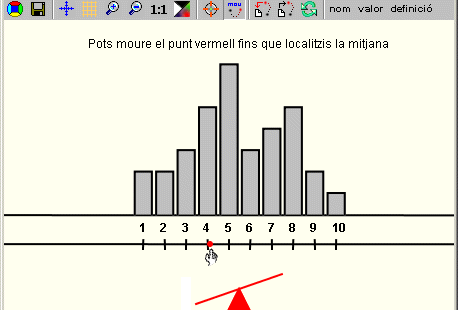
Exercitació interactiva per fer entenedor el concepte de mitjana
com a centre de gravetat
|
| |
|
| |
En acabar de fer l'exercici, és el moment d'estudiar-ne el codi
i veure que s'ha pogut elaborar una activitat de clara utilitat didàctica
sense massa necessitat de recórrer a codis sofisticats.
Torneu a engegar l'activitat, tanqueu el tauler gràfic i concentreu-vos
en el codi que es presenta estructurat en diversos apartats.
- En el primer apartat es defineix el conjunt de dades; si es vol canviar
l'aparença del diagrama de barres que heu vist, heu de modificar
aquestes dades.
- En el segon apartat se centra el tauler en el punt (5,0) i s'estableixen
algunes condicions de presentació. El fet que el tauler se centri
en el punt (5,0) fa que, si voleu modificar el perfil del diagrama de
barres, sigui recomanable canviar només les freqüències,
no les dades (el que tècnicament calcularem com el suport del
divisor).
- Tot seguit, trobareu la construcció del diagrama de barres,
amb l'eix horitzontal i els rètols. Analitzem la construcció
de les barres:

- amb x en suport en A: dibuixarem una poligonal per cada
valor observat; recordeu que aquests valors observats són
el suport(A), en aquest cas {1, 2, 3..., 10}.
- poligonal: hem situat la línia base a y =
-1; hem donat a cada barra una amplada
de 0,8 (i per això se suma i es resta 0,4 a cada valor de
x); vegeu que l'altura de cada barra és A(x),
és a dir, la freqüència observada per a la dada
x.
Pel que fa al dibuix de l'eix horitzontal i les barres, vegeu que les
barres es dibuixen com un tot i que, curiosament, una poligonal es pot
omplir.
Finalment, vegeu amb detall la construcció d'una capsa_de_text
múltiple que inclou, alhora, tots els rètols. Adoneu-vos
que els atributs de dibuix s'inclouen en la definició de la capsa
de text.
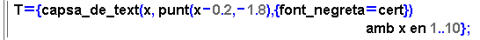
- L'apartat següent construeix i dibuixa el regle per on es mourà
el punt vermell per fer l'estimació de la mitjana. Analitzeu-ho,
amb el benentès que es fa servir la comanda segment amb
la idea de construir un segment orientat: es dóna el punt origen
i el vector que defineix el segment.
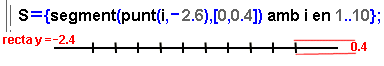
- Després es fa un procediment que ja heu vist altres vegades:
el punt vermell es mou, mitjançant la comanda punt_més_proper,
pel regle graduat i la seva abscissa és el valor que serveix
per fer l'estimació de la mitjana.
Ben segur que no presenta dificultat entendre la programació
que fa que s'escrigui un missatge de felicitació quan s'ha encertat
l'estimació:
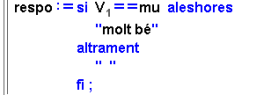
Heu de tenir ben present que la comprovació de la igualtat que
hi figura es fa amb un grau de tolerència que s'ha definit prèviament.
Podeu provar que si poseu una tolerància menor (és a dir,
si sou més estrictes) difícilment trobareu el valor veritable
de la mitjana.
- La darrera part és el dibuix de la balança, que hem
inclòs com un exemple de gràfic condicionat pels valors
d'una variable. Com ja podíeu esperar, a aquesta altura del desenvolupament
del curs s'ha de construir l'objecte fent servir les sentències
condicionals i finalment només hi ha una comanda de dibuix per
a aquesta part.

Esperem que els diversos aspectes que acabem de comentar, ben interessants
alguns d'ells, us ajudin a trobar idees primer per al projecte d'activitat
didàctica amb ús de la Wiris que heu de fer i, posteriorment,
per a la materialització del projecte, és a dir, per al desenvolupament
del vostre treball de fi de curs. |
| |
|
|
|
Interpretació del coeficient de correlació
lineal |
| |
|
| |
Activeu la pantalla següent i jugueu-hi una mica. Podeu experimentar
sobre el núvol de punts d'un conjunt de 20 dades estadístiques
bivariants, on podreu moure lliurement els punts i, en cada moment, es
mostrarà el valor del coeficient de correlació lineal (de
Pearson), unes paral·leles als eixos de coordenades fetes pel punt
mitjà de la distribució i també la recta de regressió.
|
|
|
|
| |
La part fonamental del codi que permet elaborar ràpidament
l'activitat que heu vist
|
| |
Després de practicar una estona, tanqueu el tauler gràfic
de l'activitat i quedeu-vos amb el codi. Tot seguit se n'expliquen els
detalls:
- La primera part defineix les condicions del tauler, la posició
inicial dels punts (ja hem dit al principi que la manera d'entrar les
dades no era àgil!), el conjunt dels punts, el conjunt de valors
de la primera coordenada i el conjunt de valors de les segones coordenades.
- Tot seguit es calculen les mitjanes de cada variable, el punt mitjà
de cada distribució i les paral·leles als eixos per aquest
punt. Vegeu-ho; segurament no tindreu problemes en veure per què
es fa així.

- I després, ja trobareu la part fonamental del programa, que
hem reproduït més amunt. Fixeu-vos que hem de dibuixar els
punts individualment. Per què no podríem posar abreujadament
dibuixa(A,...)? Perquè llavors el dibuix consideraria
A com un objecte únic i no podríem moure el spunts
que és justament el que volem!
- El càlcul de la recta de regressió i el coeficient de
correlació i la seva mostra en el tauler gràfic segur
que són aspectes ben entenedors.
En la mateixa línia que guia tot el treball d'aquest darrer mòdul,
saber donar idees per al projecte final (en aquest cas, una manera senzilla
d'enllaçar les vostres finestres actives), es presenta tot seguit
una aplicació didàctica a l'entorn del tauler gràfic
anterior. Es compon de cinc activitats que tenen com a objectiu didàctic
la comprensió del significat del coeficient de correlació
lineal i sobre alguns aspectes de la relació entre variables que
no contempla el coeficient de correlació i, alhora, la reflexió
que fer estadística amb poques dades és sempre perillós.
S'ha enllaçat de manera elemental des d'una pàgina de presentació
cap a la primera activitat, d'aquesta a la segona, etc.
Si en voleu consultar el codi HTM amb el Dreamweaver, sapigueu que són
les pantalles corregl.htm, corregl1.htm..., corregl5.htm, que,
si us heu baixat el material del curs respectant l'estructura de carpetes
i directoris, les teniu a .../d112/d112m7/pantalles/.
Les característiques comunes són:
- En cada pàgina hi veureu un text breu i la finestra activa.
Ara bé, si consulteu el codi, constatareu que està amagada
del tot (WIDTH=0, HEIGHT=0) i, per això, quan es visualitza l'activitat
amb el navegador, no es veu en absolut el codi, sinó que s'obre
automàticament el tauler gràfic (aquesta és la
precaució que hem hagut de tenir en gravar la pàgina de
la Wiris que hem comentat suara).
- També veureu que des de cada activitat s'enllaça a la
següent i així es llegeix la nova explicació i, com
que es torna a llegir la miniaplicació (applet) original,
cada activitat comença amb els punts del núvol de punts
en la mateixa posició que estaven al començament.
Com ja hem comentat en un altre mòdul, hi ha la possibilitat d'inserir
en una pàgina web un codi del JavaScript que fa que es pugui obrir
una pantalla de la mida més adequada. Tot i que és, evidentment,
un tema
d'ampliació, és molt interessant per presentar adequadament
activitats que tenen tauler gràfic. |
| |
|
|
|
Si cliqueu a la icona de l'esquerra, podreu
veure la manera que s'acaba de comentar de presentar una activitat didàctica
per experimentar amb el tauler gràfic anterior.
Accedireu a cinc propostes successives, redactades com una activitat
didàctica per a alumnes, amb la finalitat que reflexioneu pel que
fa als aspectes següents:
- No es poden treure conclusions rigoroses de l'estadística bivariant
feta amb poques dades. Un canvi en un valor atípic pot fer variar
substancialment el valor del coeficient de correlació.
- La disposició dels punts en els quadrants determinats per les
paral·leles als eixos dibuixades pel punt mitjà de la
distribució ens ajuda a interpretar el signe del coeficient de
correlació.
- El coeficient de correlació lineal estudia, com el seu nom
indica, la tendència a la consistència del model lineal
per representar la relació entre dues variables. El valor del
coeficient de correlació no indica res sobre altres tipus de
relació.
- El signe del coeficient de correlació i el del pendent de la
recta de regressió coincideixen, cosa que no implica res sobre
els seus valors absoluts.
- L'existència de subpoblacions clarament diferenciades en un
conjunt de dades treu tota significació estadística al
coeficient de correlació.
|
| |
|
| |
|
 |
| |
|
| |
|