|
|
Probabilitat |
| |
|
|
|
L'objectiu d'aquesta pràctica és, com el de totes les d'aquest
mòdul, donar idees.
- Donar la idea que la Wiris pot abastar des d'un punt de vista didàctic
tots els continguts de les matemàtiques de les etapes d'educació
secundària, centrant-nos en aquesta pràctica en el món
de la probabilitat.
- Donar-vos idees per al projecte i desenvolupament del treball de fi
de curs, no tant pel que fa al contingut curricular, sinó des
del punt de vista dels recursos a l'abast per muntar les activitats.
En aquest aspecte, torna a ser fonamental l'ús de les llistes.
|
| |
|
| |
Una simulació amb la Wiris per fer visual la
llei empírica de l'atzar
|
| |
|
|
|
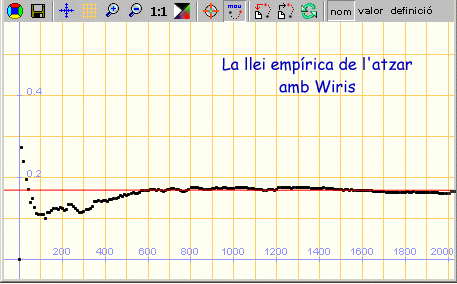
La llei empírica de l'atzar |
| |
|
| |
Per a la introducció didàctica del concepte de probabilitat
és fonamental poder fer simulacions.
A partir de les simulacions, constatarem el fet que si es fan moltes
repeticions d'una experiència aleatòria, la freqüència
relativa del nombre d'èxits d'un esdeveniment tendeix a estabilitzar-se
entorn a un valor fix: la probabilitat de l'esdeveniment. Aquesta és
la llei empírica de l'atzar i, com a empírica que
és, només la podrem comprovar amb l'experimentació.
Veurem tot seguit que la Wiris també ens pot ajudar en aquesta
tasca.
|
|
|
És clar que per fer simulacions ens cal una taula de nombres aleatoris...
o la possibilitat de generar-los amb l'ordinador. Aquest és el
cas.
Amb la calculadora Wiris tenim diverses possibilitats de generació
de nombres aleatoris seguint una distribució uniforme. La funció
aleatori és un nou exemple de funció
que, segons els arguments, retorna una resposta o una altra.
- En aquesta pràctica, fem servir aleatori(n)
on n és un nombre natural. Aquesta funció ens retorna
un nombre aleatori del recorregut 0..n-1.
- També es pot fer aleatori(m..n)on
m i n són nombres enters i la resposta serà
un nombre aleatori del recorregut m..n.
Podeu observar que 1 + aleatori(n)
(opció que s'ha seguit en la pràctica) és equivalent
a aleatori(1..n).
- En altres ocasions pot interessar obtenir un nombre aleatori corresponent
a una variable contínua. Això també és possible
amb la comanda aleatori. Podeu consultar l'índex
alfabètic de l'ajuda de la Wiris per veure'n els detalls.
Les primeres línies del codi de l'activitat didàctica que
ara podreu analitzar servirien, per elles soles (tot i que després
no tenen incidència directa en la llei empírica de l'atzar),
per constatar quina és la influència de l'atzar en els resultats
d'una experiència aleatòria.
- En la primera línia es generen 200 nombres aleatoris del conjunt
{1, 2, 3, 4, 5, 6}. Hem simulat, doncs, 200 tirades d'un "dau perfecte".
- En la segona línia la comanda compta_element ens permet
elaborar la taula de freqüències dels resultats que s'han
observat.
- Com que el resultat de compta_element (un divisor) s'ha assignat a
una variable, en la tercera línia veiem com es pot fer per obtenir
el recompte del nombre de sisos que han sortit.
- Si obriu la Wiris
 ,
escriviu les tres línies que s'han comentat i repetiu diverses
vegades el càlcul, veureu les diferències que s'observen
d'una vegada a l'altra. ,
escriviu les tres línies que s'han comentat i repetiu diverses
vegades el càlcul, veureu les diferències que s'observen
d'una vegada a l'altra.
- Per fer visual la llei empírica de l'atzar, haurem de repetir
un procediment com el que acabem de comentar, però no per al
total de tirades, sinó per cada nombre de tirades, i observar
què passa quan aquest nombre de tirades va augmentant.
Com en altres ocasions, ara us proposem primer de tot que feu l'activitat
i després ja n'analitzraem el codi. Cliqueu a la icona de la fletxa
que teniu a continuació i repetiu l'experimentació per veure
novament les diferències d'una simulació a una altra.
- Recordeu que per repetir l'activitat no cal que tanqueu el tauler
on s'ha mostrat el gràfic (però segurament és més
clar fer-ho); heu de posar el cursor en una de les línies que
tenen el codi de l'activitat i fer clic a la icona de la fletxa (o també
Control + Retorn).
|
| |
|
|
|
|
| |
Amb la Wiris podem simular les tirades d'un dau i fer recomptes
|
| |
|
|
|
Vegem el codi que ha permès fer l'activitat anterior.
Ja hem comentat que les primeres línies generen 200
tirades d'un dau i compten quants sisos han sortit. Però no ens
interessa veure-ho en el total de les 200 tirades, sinó per cada
nombre de tirades de l'1 al 200. Per això es construeix una llista
Frel que en el lloc i hi té la freqüència
relativa del nombre de sisos que han sortit en les i primeres tirades.

- Aquesta llista Frel es mostra en pantalla,
tot i que no seria, en absolut, necessari, però és un
complement a la visualització gràfica. Si els nois i les
noies confronten la llista LL amb els resultats de les tirades
del dau amb la llista Frel amb les freqüències relatives
del nombre de sisos, ben segur que això serà un ajut per
entendre què estem calculant.

Ara ja només falta fer el dibuix; es comença
per definir el tauler:
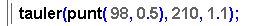
- No es canvia la mida de la finestra: serà de 450 x 450, com
és habitual.
- S'estableix que l'eix de les x abasti una graduació
de 210 unitats (de l'1 al 200, que és l'interval que ens inetressa
per fer el gràfic i una mica més). Semblantment amb l'eix
de les y: els valors observats varien de 0 a 1, es dóna
una mica de marge.
- Es defineix el centre del tauler perquè el gràfic quedi
situat com ja heu vist en l'exercitació de l'activitat.
Ben segur que ja no teniu cap problema en la intepretació de les
ordres finals:
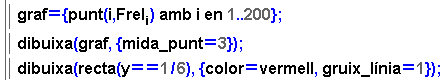
Es construeix la llista graf de punts que volem dibuixar. Fixeu-vos
que, com que Frel és una llista, Freli
és l'element de lloc i en aquesta llista. No seria vàlida
la notació Frel(i) com si treballéssim amb una funció.
Tot seguit, es dibuixa la gràfica i també es dibuixa la
recta que mostra l'estabilització de la Frel entorn del
valor de la probabilitat (o no la mostra en alguna simulació, tot
depèn de l'atzar!).
Aquest darrer comentari i totes les observacions de les grans diferències
que veieu d'una simulació a una altra porten, naturalment, a dir
que 200 tirades són molt poques per constatar la llei empírica
de l'atzar.
Què caldria fer per augmentar el nombre de tirades a 500, posem
per cas? A banda de modificar les dimensions de la pantalla (cosa que
si us interessa podeu llegir com es fa en l'enllaç anterior a un
tema d'ampliació, la icona de la lupa), hauríeu de canviar
les línies següents:
- En la primera línia, en la que diu per j
en... i en la que defineix graf podeu posar 1..500 en
lloc de 1..200.
- El tauler el podeu definir així: tauler(punt(245, 0.5),
520, 1.1).
Feu aquestes modificacions i altres proves i, si us interessa el tema,
podeu trobar una proposta d'exercici voluntari...
o potser la gènesi d'un projecte per al treball final!
|
| |
|
|
|
La distribució normal |
| |
|
| |
Si engegueu l'activitat següent de la manera habitual, podreu fer
algunes reflexions de caràcter didàctic sobre la distribució
normal a partir d'una gràfica inicial, que és justament
la de la funció de densitat de probabilitat de la distribució
normal estàndard.
- Tal com s'indica a la imatge, si moveu els punts negres que determinen
un segment a la part inferior del tauler gràfic, podreu variar
la mitjana (indicada per l'eix de simetria, recta de color verd) i la
desviació estàndard de la distribució, i la gràfica
s'actualitzarà.
- Si moveu els dos punts vermells que teniu sobre l'eix de les x,
canviareu l'interval de què es calcula la probabilitat. Ja sabeu
que aquesta probabilitat és l'àrea de la zona acolorida
de color vermell.
Experimenteu-hi!
|
|
|
|
| |
|
| |
Us recordem que podeu ampliar manualment la part visible de la finestra.
Pot ser interessant que en aquest cas ho feu amb l'eix horitzontal per
a algunes de les activitats que us aconsellem:
- Comparació de gràfiques amb la mateixa mitjana i diferents
desviacions estàndards.
- Comparació de gràfiques amb la mateixa desviació
estàndard i diferents mitjanes.
- Amb la gràfica de la normal estàndard: visualització
de la probabilitat dels intervals [-1, 1],
[-2, 2] i [-3,
3] que s'acostumen a considerar característics de la distribució
normal.
- Idea de l'estandardització: vegeu que la probabilitat de l'interval
[0,5; 1,5] amb la distribució normal estàndard és
la mateixa que la probabilitat de l'interval [1,5; 3,5] en la distribució
normal que té mitjana 0,5 i desviació estàndard
2. Els valors 1,5 i 3,5 són, en aquest cas, els que disten de
la mitjana, respectivament 0,5 i 1,5 desviacions estàndards.
Per això es corresponen amb els valors 0,5 i 1,5 de la normal
estàndard.
|
| |
A continuació, es comenten alguns aspectes del codi amb què
s'ha preparat l'activitat. El podreu consultar fàcilment si engegueu
i tanqueu el tauler gràfic.
-
La funció que defineix la densitat de probabilitat
de la distribució normal és:
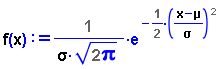
- Les primeres línies del codi es destinen a definir la interactuació
que es pot fer per definir els valors de la mitjana i la desviació
estàndard, juntament amb la recta que serà l'eix de simetria
de la corba.
- Hem posat expressament una línia per comentar "que no
fa el que sembla". Segur que quan heu estat fent experimentacions
i heu variat els paràmetres definidors de la distribució
normal, heu pensat en la possibilitat que el centre del tauler s'actualitzés.
Això no és possible, perquè el tauler només
es defineix la primera vegada que es processa la comanda tauler.
Així, doncs, com que
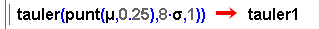
es llegeix (per primera vegada) en un moment en què m
= 0 i s = 1 és equivalent a
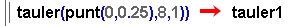
El tauler es veu tota l'estona amb aquest centre, encara que manualment
canviem l'amplada de la finestra. Recordeu, doncs: el tauler es defineix
d'una vegada per totes i no es pot actualitzar.
- La construcció de la llista dels segments que acoloreixen l'àrea
que ens dóna la probabilitat de l'interval [xm, xn] es
fa així:
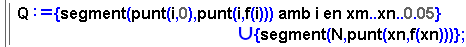
- Si es volgués que l'àrea quedés completament
acolorida, es podria substituir el 0,05 per un nombre més
petit, per exmeple, 0,01, però llavors costaria froça
actualitzar el dibuix. Proveu-ho i considereu si us sembla un valor
afegit.
- S'afegeix el segment que tanca per la part dreta, perquè
si no es fes així, potser el salt de 0,05 faria que no es
passés exactament per xn i llavors l'efecte visual
no seria correcte.
-
Potser us heu adonat que quan s'executa la finestra de la Wiris que
inclou aquesta activitat, surt un missatge d'avís (indicat
per un requadre verd). Per què?
Quan una pantalla de la Wiris s'ha gravat sense la barra d'eines
(com és el cas), tampoc mostra la finestra d'errors. Però
amb el botó dret del ratolí, podeu recuperar-les en
posició flotant. Si ho feu, llegireu de què us vol avisar
el programa:
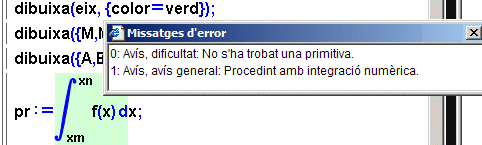
Efectivament, els valors de la probabilitat d'un interval segons
la distribució normal de probabilitat s'han de fer per integració
numèrica!
És, justament, la integral 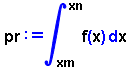 la que ens dóna aquesta probabilitat.
la que ens dóna aquesta probabilitat.
-
Ben segur que entendreu tot allò que no es comenta. Si no
fos així, ja sabeu que podeu preguntar-ho!
|
| |
|
 |
| |
|
| |
|