|
||||||||||||||||
| Pràctica |
|
Exercicis
|
||||||||||||||
| Mostra d'unitats didàctiques
|
||||||||||||||||
| Llibreries en una sessió de treball de la Wiris | |
|
En aquesta darrera pràctica del curs es comenta la possibilitat de definir llibreries i es presenten tres exemples d'ús d'aquest recurs. És una possibilitat que s'ha de tenir en compte, perquè potser us pot ajudar en algun aspecte del vostre treball de fi de curs. I ja des d'ara us animem a ampliar la llibreria-teca que trobareu al Racó de la Wiris, on veureu els tres exemples d'aquesta pràctica i altres que s'hi hagin incorporat per la col·laboració del professorat. Ànim! |
|
|
|
Què és i com s'estableix una llibreria |
|
En una finestra de treball de la Wiris es poden definir llibreries.
En aquesta definició ja hi consten dos aspectes que es veu de seguida que poden ser molt interessants en el vostre treball a classe amb la Wiris:
|
|
| Podeu clicar a la icona de l'esquerra per veure una animació que explica com es pot generar una llibreria. | |
| Vegeu en la imatge següent com s'ha definit la llibreria que apareix en l'animació anterior i s'està a punt de fer càlculs. | |
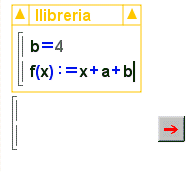 Una llibreria definida amb el codi a la vista. |
|
| Ara vegeu què passa si ja heu "tancat la llibreria". El codi que hi pertany resta amagat, però està actiu en tots els blocs de la finestra activa. | |
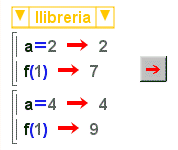 La funció f i el valor de la variable b "estan amagats", però són actius. |
|
En els apartats següents veureu tres exemples d'ús de llibreries. Ben segur que la vostra imaginació podrà treure molt de suc d'aquest recurs! |
|
|
|
Passar a graus, minuts i segons |
|
|
Algunes preguntes de la primera edició del curs D112 feien referència
a la no-existència dins la Wiris d'una funció que fes una
tasca semblant a la de la tecla Esudieu per què la funció que passa un nombre x que representa graus sexagesimals expressats com un nombre decimal a la corresponent mesura en º ' " (graus, minuts i segons sexagesimals, arrodonint els segons) és:
Adoneu-vos que la funció gms (amb una decisió encertada o no, això cadascú ho pot jutjar) rep un nombre i retorna una expressió complexa amb unitats. |
|
A la pantalla activa que s'obre si cliqueu a la icona de l'esquerra,
hi teniu una llibreria amb la funció gms i dues més, rg,
que passa un nombre de radiants a una mesura en graus sexagesimals, i
rgms, que transforma un nombre de radiants en una mesura complexa
en També hi teniu tres exemples d'aplicació que mostren la vigència de les funcions de la llibreria en tota la finestra activa.
|
|
|
|
Dibuixar vectors |
|
Obriu la finestra de la Wiris que s'activa amb la icona de l'esquerra. Potser pensareu: "Però si no fa res!", i és que està preparada perquè definiu una llibreria!
|
|
|
Una llibreria amb dues versions per dibuixar un vector. |
|
|
I una vegada definida la llibreria, podeu comprovar que els altres blocs de comandes "ja treballen":
Però l'important d'aquest apartat era en general la llibreria i veure com actuava. Si ara voleu tenir una llibreria de vectors a punt per aprofitar-la des del punt de vista gràfic en les vostres activitats amb vectors, només cal que esborreu totes les línies que no formen part de la llibreria i guardeu la finestra activa amb el nom que us convingui. Quan la recupereu, s'engegarà la Wiris amb la vostra llibreria a punt. |
|
|
|
Sobre nombres aleatoris |
|
Suposeu que voleu plantejar amb la calculadora Wiris una prova ben senzilla de càlcul. Quelcom semblant al que es veu a la imatge següent, però de manera que els nombres que apareguin siguin aleatoris.
La funció aleatori(n) de la Wiris dóna un nombre enter en el recorregut 0 .. n-1. Llavors una manera d'aconseguir (aparentment) l'activitat anterior amb nombres en l'interval -5..5 és:
Però si feu que es calculi per saber el valor dels nombres amb què heu d'operar, lògicament dóna error.
I llavors, ai las!, si escriviu el resultat i feu que es recalculi, canvien els nombres! Aquesta és la particularitat de la Wiris: en cada recàlcul es regeneren els nombres aleatoris.
Llavors hom pensa en les llibreries. Per una banda, permetrien amagar a l'alumna o l'alumne a qui li plantegeu el càlcul el codi aleatori de la funció que pot ser que emboliqui més que no pas ajudi. I per l'altra, es conservaria llavors el valor de A, B, C?
Podríeu tancar la lliberia i tindríeu ben bé el que es proposava al principi. Però, tanmateix, tots els altres problemes de canvi en el valor dels nombres aleatoris es mantenen. Tot seguit presentem una llibreria que, entrant un nombre enter, dit llavor, permet generar nombres aleatoris que en cada recàlcul siguin els mateixos... fins que canvieu la llavor! Hom pensarà que per a un problema senzill com l'anterior això és com "matar mosques a canonades", però tingueu ben present que del que es tracta és de donar idees per a les vostres aplicacions didàctiques. I, molt concretament, si voleu generar un gràfic intercatiu que inicialment tingui unes components aleatòries (però que el gràfic es mantingui en tota la interacció), llavors aquesta llibreria us pot servir! |
|
|
En aquest cas no us donem una pantalla activa amb el codi. En podeu entendre el funcionament si mireu l'animació que s'engega tot clicant a la icona de l'esquerra, i escriure el codi (que teniu reproduït a la imatge següent) us pot ajudar a copsar millor el quid de la qüestió.
Adoneu-vos del funcionament del programa, amb el benentès que l'objectiu és conèixer les possibilitats que ofereixen les llibreries, no pas buscar la manera més eficient i elegant de resoldre el problema que us ocupa.
I com es poden generar nombres aleatoris? S'ha fet servir l'anomenat mètode multiplicatiu que, prenent com a dades bàsiques un nombre primer m i un nombre u < m i a partir d'un nombre llavor (un altre nombre enter positiu més petit que m) genera una llista de nombres enters pseudoaleatoris de l'interval [0, m-1].
|
|