|
||||||||||||||||
| Pràctica |
|
|
|
Exercicis
|
||||||||||||
|
|
Gràfics amb recursos avanšats de la Wiris |
|
En la prÓctica anterior heu pogut veure que l'˙s de recursos de programaciˇ aplicats a la realització de gràfics ens han permès avançar força en la interactivitat. En el mòdul 2 vam presentar les llistes com un element de treball avançat amb la Wiris que, juntament amb l'ús de amb..en..on.. per generar-les, poden substituir moltes vegades procediments que a primera vista sembla que s'haurien de fer amb la programació. Ara veurem que també va molt bÚ tenir en compte les llistes a l'hora de fer grÓfics sofisticats.
|
|
| Després d'uns exemples lúdics, analitzarem amb tot detall una activitat que ja coneixeu i completarem la pràctica amb una reflexió sobre l'ús de la comanda punt_més_proper per construir gràfics tipificats, per exemple, un quadrilàter que permeti moure (alguns) vèrtexs i sempre es mantingui com un rectangle. | |
|
|
┌s de amb..en.. per a la generaciˇ de llistes d'objectes dibuixables |
|
En la pràctica 1 del mòdul 2 heu pogut conèixer la manera de fer un gràfic que recorda el logotip del Campionat del Món de Natació - BCN 2003. Aquí teniu una possibilitat que ara explicarem:
Recordeu quin és el punt (r·cos(a), r·sin(a)) i llavors us podeu adonar que, perquè s'aconsegueixi l'efecte espiral:
Vegeu que amb les consideracions anteriors construïm una llista de circumferències que després dibuixem totes de cop i recordeu que el mètode de treball de la Wiris no permet substituir el procés anterior per quelcom que hi és conceptualment semblant, com és ara:
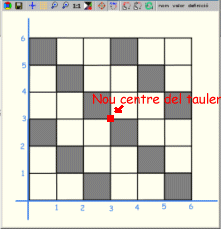
Podeu escriure el codi que us hem mostrat i fer-hi variacions. Recordeu, també, que, si volguéssiu dibuixar les circumferències de colors diferents, no seria possible fer-ho amb una sola ordre. En el segon exemple que us proposem veureu una manera de dibuixar un engraellat 6 x 6 amb algunes caselles acolorides, com aquest:
L'exemple servirà per recordar l'ús de condicionals en la generació de llistes i per explicar alguns aspectes de la comanda tauler. Si cliqueu a la icona de la fletxa, activareu una finestra de la Wiris on veureu una manera d'aconseguir l'objectiu indicat, que comença per situar els eixos i la graduació de les unitats com podeu veure en el gràfic següent. |
|
|
|
|
Us proposem que, com a exercici, feu les variacions oportunes a l'exemple que acabem de presentar per obtenir un tauler d'escacs com el que mostra la imatge il·lustrativa de la capçalera de la pràctica. |
|
| Estudi detallat d'una aplicació didàctica generada amb la Wiris | |
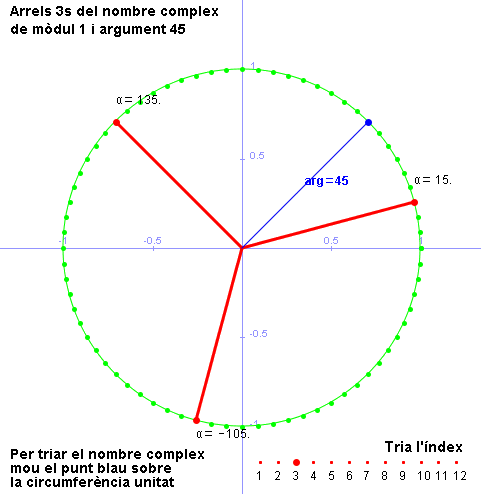
| En acabar la pràctica 6 del mòdul 2, que tracta el tema dels nombres complexos, heu pogut veure una aplicació generada amb la Wiris que s'ha presentat justament com a aplicació didàctica. Podeu revisar-la tal com l'hem presentat allà si cliqueu a la icona que indica el començament de l'activitat o bé a la mateixa imatge. | |
|
|
|
|
Ara ha arribat el moment d'estudiar amb detall el codi d'aquest exemple. Veurem l'aplicació de amb..en per a la generació d'objectes sofisticats que després dibuixarem; veurem l'ús de la comanda punt_més proper i, combinant-ho, aprendrem a incloure en un tauler gràfic un menú d'opcions que, en aquest cas, farem servir per triar l'índex de l'arrel. Tot seguit, podeu obrir una finestra activa amb el codi molt detallat i comentat. Podeu anar-la consultant mentre llegiu les explicacions que teniu més avall. |
|
|
|
|
Segur que amb aquestes indicacions i una bona dosi de paciència per a l'anàlisi ja heu tret l'entrellat del codi que analitzàvem. Ara no us en demanarem cap exercici relacionat... però ben segur que us donarà idees per a les vostres aplicacions que hauran de formar part del treball de fi de curs. |
|
|
|
GrÓfics subjectes a condicions |
|
De vegades, en les aplicacions didàctiques és interessant que una figura compleixi sempre unes determinades condicions. En la pràctica 6 del mòdul 1 ja vam veure la construcció interactiva d'un paral·lelogram. Es podien moure tres dels vèrtexs i la figura sempre es manetnia com a paral·lelogram. El quart no era lliure, no el podíem controlar, sinó que era el que ens ajudava a aconseguir que el quadrilàter fos un paral·lelogram. Us proposo, tot seguit, que analitzeu l'exercici de dibuixar un quadrilÓter
que sempre sigui un rectangle... per˛ naturalment no tots els vŔrtexs
es podran moure lliurement. Vegeu-ne primer de tot una animació. |
|
I ja podeu ordenar de fer el dibuix, posar algun rètol explicatiu... i provar si funciona. |
|
| I si no ha sortit bé, podeu fer clic a la fletxa de l'esquerra i veureu una manera de fer el codi d'aquesta activitat seguint les instruccions anteriors que sí que funciona. | |
| Consulteu-lo i us servirà, perquè a la llista d'exercicis d'aquest mòdul, trobareu com a proposta opcional la construcció d'un quadrilàter que sempre sigui un rombe. | |