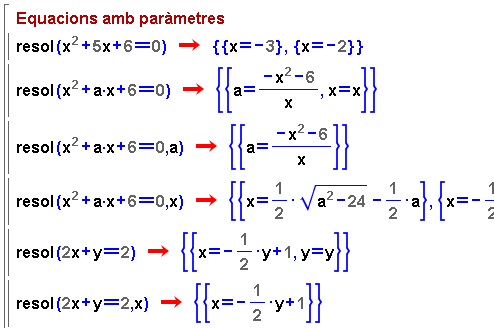|
|
Resolució d'equacions |
| |
|
|
|
En aquesta pràctica, aprofundirem en les comandes resol
i resol_numèricament per trobar les solucions
d'una equació, que ja es van introduir en la pràctica
3 del mòdul 1.
Veurem:
- l'aplicació de mètodes numèrics a la resolució
d'equacions
- una aplicació didàctica per visualitzar/interpretar
gràficament les solucions d'una equació
- la manera com la Wiris treballa amb equacions que tinguin més
d'una variable
- els recursos per a obtenir els valors de les solucions i assignar-los
a variables de memòria per a càlculs posteriors. Per a
això estudiarem l'estructura de llista de taules en què
la Wiris ens presenta les solucions d'una equació.
|
| |
|
| |
|
| |
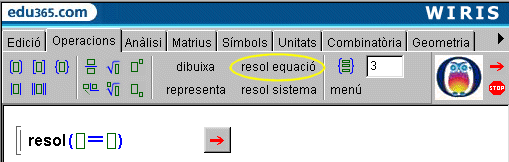
Situació de la icona que facilita l'escriptura de la comanda que
resol equacions
|
| |
|
|
Escriure una equació i obtenir les solucions |
| |
|
|
|
Convé recordar alguns aspectes que ja es van comentar en el mòdul
1.
Per escriure correctament una equació, cal separar les dues parts
que la formen amb el signe d'igual llarg, que equival a dos signes d'igual,
i que també és pot obtenir amb la icona  de la pestanya
de la pestanya  i també apareix amb la combinació de tecles
i també apareix amb la combinació de tecles
Control + Igual.
- Perquè la Wiris resolgui l'equació, cal escriure l'equació
entre parèntesis dintre de la comanda resol
o resol_numèricament.
Direm que passem l'equació com a argument de la comanda corresponent.
- Per facilitar la tasca d'escriptura, a la barra d'eines de la Wiris
trobareu la icona
 a la carpeta de la pestanya
a la carpeta de la pestanya  .
Fent clic en aquesta icona, s'escriurà a la finestra activa la
comanda .
Fent clic en aquesta icona, s'escriurà a la finestra activa la
comanda

i ja tindreu els parèntesis, l'igual llarg i el nom de la comanda.
Ara només caldrà entrar a les caselles i escriure els
dos membres de l'equació. Es pot passar d'una casella a l'altra
amb les tecles del cursor.
- Si feu servir la icona
 i voleu resoldre l'equació per mètode numèrics,
només cal editar la comanda per introduir _numèricament
després d'haver clicat a la icona.
i voleu resoldre l'equació per mètode numèrics,
només cal editar la comanda per introduir _numèricament
després d'haver clicat a la icona.
- Quan el segon membre de l'equació és 0, no cal escriure
resol(expressió==0);
es pot indicar, simplement resol(expressió).
Recordeu una diferència fonamental:
- La comanda resol (que també es pot
indicar com resoldre) intenta buscar totes
les solucions d'una equació, per mètodes exacates o aproximats.
Per exemple, ens dóna sempre totes les solucions d'una equació
polinòmica com veurem amb detall a la pràctica
següent. També veurem que, en aquest cas, tenim la comanda
arrels, que ens retorna les solucions com
una única llista de valors.
- En canvi, la comanda resol_numèricament
(que també es pot expressar resoldre_numèricament)
busca una solució (que no sempre serà la que ens interessa).
Les solucions trobades es tornen en forma d'una llista, que serà
buida -{}- si no se n'ha trobat cap. Més
endavant es comenta l'estructura formal dels conjunts de solucions.
|
| |
|
|
Equacions de primer grau: la resposta de la
Wiris |
| |
|

|
Obriu la següent finestra activa de la Wiris, clicant la icona de
l'esquerra. Executeu les comandes i observeu la resposta de la Wiris en
cada cas possible, segons el nombre de solucions. Useu la icona  per introduir noves equacions i comprovar com treballa la Wiris.
per introduir noves equacions i comprovar com treballa la Wiris.
|
| |
|
| |

|
| |
Comandes de la finestra activa anterior
|
| |
|
|
Resolució d'equacions per mètodes
numèrics |
| |
|
|
|
- La Wiris incorpora diversos mètodes numèrics per a
la resolució d'equacions. En cada cas, selecciona el més
apropiat i intenta trobar una solució a partir d'un punt o un
interval inicial.
- La comanda per resoldre equacions amb aquests mètodes és
resol_numèricament i la podem entrar
tal com s'ha explicat amb la comanda resol,
afegint a mà l'acabament "_numèricament".
- Remarqueu que el fet de buscar una única
solució de l'equació fa que els resultats obtinguts
siguin d'una natura diferent als obtinguts amb la comanda resol:
mentre la comanda resol torna una llista de
llistes, la comanda resol_numèricamentnomés
retorna una llista. Al final d'aquesta pràctica, aprofundirem
en l'estructura de les solucions.
|
| |

|
| |
Diferències sintàctiques entre resol
i resol_numèricament
|
| |
|

|
Obriu la finestra activa clicant a
la icona de l'esquerra i executeu les comandes per veure l'estructura de
les solucions. |
| |
|
|
Trobar la solució que volem per mètodes
aproximats |
| |
|
|
|
A la finestra activa anterior heu vist una equació amb una solució
evident que la Wiris no sap trobar. Per trobar les solucions que ens interessen,
hem de conèixer el mecanisme intern de la Wiris:
- Per defecte, la Wiris utilitza un mètode recurrent amb un
valor inicial de la variable. Veureu la sintaxi adequada per
donar un punt inicial i trobar totes les solucions de l'equació
esmentada en la propera finestra activa de la Wiris.
- Segurament, ja sabreu que no sempre és fàcil encertar
el valor que permet acostar-se a la solució que volem. Per això,
també hi ha una altra possibilitat (més lenta, però
segura i robusta) en què podem escriure l'interval on volem trobar
la solució. Cal indicar, a més, el
mètode i heu de tenir present que, per a la correcta aplicació,
cal que la funció prengui valors diferents en els dos extrems
de l'interval.
|
| |
|

|
Obriu la finestra activa clicant
a la icona de l'esquerra i executeu les comandes per veure la forma de donar
el valor inicial i el mètode de resolució i per observar la
solució obtinguda en cada cas. |
| |
|
| |
|
| |
A la recerca de totes les solucions d'una equació
|
| |
|
|
|
- Localizeu les solucions principals de l'equació sin
x + 2 cos x == 1 per mètodes aproximats, entrant les comandes
necessàries en el segon bloc de la mateixa finestra activa anterior.
- A vegades, va bé localitzar primer les solucions d'una manera
visual, tal com s'explica en la finestra activa que es presenta en l'apartat
següent.
- Podeu desar la finestra activa de la Wiris tal com s'explica en la
pràctica 1 del
mòdul 1.
|
| |
|

|
Si voleu ampliar el tema i saber quins són
els mètodes numèrics disponibles per a la comanda resol_numèricament,
feu clic a la icona de l'esquerra. |
| |
|
|
|
Interpretació gràfica de les
solucions d'una equació |
| |
|
|
|
En la finestra activa que podeu obrir amb la icona
habitual teniu un exemple que visualitza gràficament les solucions
de l'equació que hem treballat a l'apartat anterior i genera un
tauler interactiu com el de la imatge següent.
Estudieu el funcionament de l'activitat i el codi que la genera. En aquest
cas, podreu veure la utilitat que en molts moments pot tenir afegir comentaris
en una finestra de treball de la Wiris amb la icona  .
Això us pot donar idees per a la presentació de les vostres
activitats didàctiques. .
Això us pot donar idees per a la presentació de les vostres
activitats didàctiques.
|
| |
|
|
|
|
| |
El tauler gràfic ens pot ajudar a trobar els valors inicials per
a la resolució numèrica d'una equació
|
| |
|
| |
- Obriu la finestra activa de l'esquerra i modifiqueu les fórmules
de les funcions per visualitzar les solucions de l'equació 2^x
== x+5 o bé, si us interessa treballar amb continguts més
elementals 3x + 5 == -2x
+1 i podreu experimentar per trobar gràficament la solució.
- Deseu la finestra activa de la Wiris, usant la icona
 de la pestanya
de la pestanya  i les instruccions que ja coneixeu i que podeu revisar en la primera
pràctica del
curs.
i les instruccions que ja coneixeu i que podeu revisar en la primera
pràctica del
curs.
|
| |
|
|
Equacions amb paràmetres |
| |
|

|
Una equació pot tenir una o més
variables. Si no especifiquem quines variables volem aïllar en funció
de les altres, la Wiris interpreta que volem usar totes les variables que
apareixen a l'equació. Vegeu el comportament de la Wiris en els exemples
de la finestra activa que trobareu clicant a la icona de la dreta. |
| |
|
| |
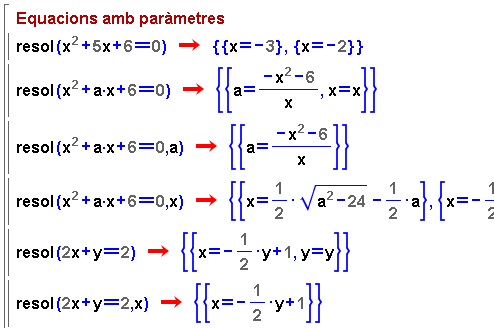
|
| |
Exemples d'equacions amb paràmetres
|
| |
|
|
|
En l'exemple anterior, observeu la necessitat
del punt de multiplicar entre les variables a i x, ja que
si oblideu el punt, la Wiris interpreta que ax és una única
variable, cosa que no passa amb l'expressió 5x, atès
que els noms de les variables no poden començar amb un número. |
| |
|
|
|
Estructura sintàctica de les solucions |
| |
|
|
|
De la mateixa manera que quan parlàvem de la descomposició
en factors primers, això ens ha servit per presentar, com a ampliació,
un objecte estructurat de la Wiris anomenat divisor, ara, enllaçant
amb la conveniència d'aprofundir en les possibilitats de treball
amb equacions i sistemes i poder aprofitar per a altres càlculs
els valors de les solucions, ara podeu estudiar la manera com se'ns retorna
el resultat de la comanda resol, que aprofita un objecte de la
Wiris que es designa com a taules.
|
| |
|
| |
- Una taula és un objecte de la Wiris format per una llista
de parelles x=a on x
és un identificador i a
un valor o objecte de la Wiris. Per entendre el significat d'una
taula, podem pensar que és un recurs per poder assignar el valor
a a l'identificador x
mitjançant recursos estructurals i sintàctics.
- Són exemples de taules M ={gener=1,
febrer=2,
..., desembre=12},
{c=punt(1,2),
=5},
o bé S={x=1,
y=2,
z =-1}.
- Per obtenir el valor que una taula assigna a un identificador, cal
aplicar la taula a l'identificador, com si es tractés d'una funció.
- Si l'identificador consta a la taula, la resposta és el
valor corresponent.
- Altrament, és a dir, si l'identificador no apareix a la
taula, la resposta és nul.
- Vegeu-ne exemples:
M(abril)=4, M(february)=nul,
S(x)=1, S(t)=nul,
3·S(x)+4·S(y)-2·S(z)=13
Les solucions d'una equació amb la comanda resol apareixen com
una llista de taules.
- Cada una d'aquestes taules és una solució de l'equació.
- En cada una d'aquestes taules apareixen parelles x=a
, on x és la variable que apareix a
l'equació i a el seu valor per a aquella
solució.
- El fet que l'estructura de taula permet assignar a l'identificador
x que és el primer element de la parella
x=a el valor a fa
que hi hagi una manera equivalent de presentar aquestes solucions, que
fa servir la sintaxi x
 a. a.
Tot seguit es mostren exemples de com treballar amb els valors de les
solucions d'una equació, obtingudes amb las comanda resol,
en una finestra activa.
|
| |
|

|
Cliqueu a la icona de l'esquerra per veure dues
propostes diferents d'obtenció dels valors de les solucions d'una
equació, en una finestra activa de la Wiris. Executeu el bloc de
comandes i observeu els resultats obtinguts, dels quals a la imatge es mostra
el que es relaciona amb l'ús de les taules. |
| |
|
| |

|
| |
Una manera d'obtenir els valors de les solucions
|
| |
|
|
|
Per escriure els subíndex, es pot usar
la icona  de
la pestanya de
la pestanya  o també el teclat, marcant Control + Fletxa
avall per entrar en el subíndex. Per sortir del subíndex,
podeu marcar la tecla Fletxa dreta
o també el teclat, marcant Control + Fletxa
avall per entrar en el subíndex. Per sortir del subíndex,
podeu marcar la tecla Fletxa dreta |
| |
|
| |
|
 |
| |
|
| |
|