|
|
Inequacions |
| |
|
| |
La darrera pràctica d'aquest mòdul tracta el tema de les
inequacions. Veureu com introduir diverses inequacions amb una
incògnita i la resposta de la Wiris. També hi ha una activitat
per treballar gràficament les inequacions de primer grau amb dues
incògnites.
Els símbols necessaris per definir i treballar amb equacions o
inequacions es mostren en la taula següent. La Wiris té icones
a la pestanya  per escriure'ls; aquesta opció és la que dóna la
millor qualitat tipogràfica, però també es poden
entrar mitjançant el teclat o amb una combinació de tecles.
per escriure'ls; aquesta opció és la que dóna la
millor qualitat tipogràfica, però també es poden
entrar mitjançant el teclat o amb una combinació de tecles.
|
| |
|
| |
|
| |
|
|
|
Resolució d'inequacions |
| |
|
| |
- La Wiris resol aquelles inequacions amb una variable que permetrien
la resolució de l'equació associada amb la comanda resol.
- La sintaxi de la comanda és resol_inequació(expressió
de la inequació).
- Es poden utilitzar variables o expressions definides anteriorment.
- La Wiris retorna la solució de les inequacions mitjançant
els operadors lògics & i |.
Si apareixen els dos operadors, s'entén que &
té prioritat sobre |.
- Si l'equació no té solució, la resposta és
fals.
- Si l'inequació té per solució qualsevol valor
real de x, és a dir, si la desigualtat és certa
per a qualsevol x, la resposta és cert.
- Els exemples de la finestra següent corresponen diverses inequacions
polinòmiques.
|
| |
|
 |
|
| |
|
| |
- En el cas d'equacions polinòmiques amb solucions no senceres
cal afegir un punt a un dels coeficients de la inequació per
tal de resoldre-la.
- Proveu altres inequacions polinòmiques i afegiu un punt a un
dels coeficients.
|
| |
|
| |
|
| |
|
| |
- No existeix cap comanda equivalent a resol_numèricament
per inequacions . En el cas que no resolgui, acoloreix de color verd
la comanda resol_inequació.
- Si no troba cap solució, la resposta fals
o cert que dóna no té significació.
|
| |
|
 |
|
| |
|
| |
- Canvieu la funció per alguna altra que no resolgui numèricament
i observeu la resposta de la Wiris.
- Observeu la representació gràfica de la funció
associada a la inequació.
|
| |
|
|
|
Representació de les solucions d'una
inequació |
| |
|
| |
Una forma d'interpretar les solucions d'una inequació
amb una variable consisteix a representar la funció corresponent
i acolorir els intervals corresponents a f(x)>0 i a f(x)<0. |
| |
|
|
|
|
| |
|
| |
- Per aconseguir el gràfic de la imatge, cal definir, en primer
lloc, la funció associada a la inequació que es vulgui
estudiar i calcular els punts d'intersecció amb els eixos.
- Les llistes L i M estan formades per punts (x,
0) de l'eix d'abscisses que verifiquen la condició f(x)>0
i f(x)<0, respectivament.
|
| |
|
| |
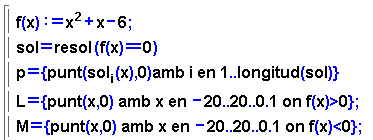 |
| |
|
| |
- El resultat gràfic de dibuixar les llistes L i M
és el de l'acoloriment dels intervals de l'eix d'abscisses corresponents
a les condicions f(x)>0 i f(x)<0.
- Per a aquest exemple s'han indicat els colors mitjançant el
codi RGB.
|
| |
|
| |
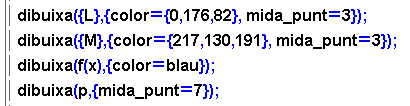 |
| |
|
| |
- Les comandes d'escriptura fan coincidir el color del text amb l'interval
corresponent.
|
| |
|
| |
 |
| |
|
| |
El resultat gràfic de l'activitat serveix
per presentar i relacionar conceptes relatius a les solucions d'una inequació.
Podeu estudiar diferents inequacions només canviant la funció
f(x). |
| |
|
|
|
Sistemes d'inequacions amb una variable |
| |
|
| |
- Un sistema d'inequacions s'introdueix en forma de llista o bé
amb l'operador lògic &.
- Es poden plantejar combinacions de diverses inequacions amb els operadors
lògics &, |
o no.
|
|
|
|
 |
|
| |
|
| |
- Observeu les dues opcions per introduir un sistema: en forma de llista
o bé amb l'operador &.
- En el darrer sistema d'inequacions interpreteu els resultats.
- Plantegeu altres inequacions i sistemes.
|
| |
|
|
|
Interpretació gràfica
d'una inequació de primer grau amb dues incògnites |
| |
|
| |
|
| |
|
| |
L'activitat següent serveix per interpretar gràficament les
solucions d'una inequació de primer grau amb dues incògnites.
Es representa una recta definida a partir de dos punts, se'n calcula l'equació
implícita
Ax + By + C = 0, i es defineix la funció de dues variables
f(x, y) = Ax + By + C.
Des del tauler gràfic, s'observa que els valors d'aquesta funció
en els punts del mateix semiplà que defineix la recta són
del mateix signe, i els de l'altre semiplà són tots de signe
contrari. Per tant, els punts de cada semiplà representen gràficament
una de les inequacions:
Ax + By + C < 0 o Ax + By + C > 0.
|
| |
|
 |
|
| |
|
| |
En la finestra activa observeu els diferents passos:
- La recta AB es defineix a partir de dos punts que es poden
moure des del tauler gràfic.
- El punt C és un punt auxiliar que s'utilitza per saber
el sentit de la desigualtat.
- La comanda equació(r) retorna l'equació
de la recta en la forma y = ax + b, o bé
x = a, si és el cas. Aquesta expressió és
una llista. El primer element de la llista és l'expressió
a l'esquerra de la igualtat, i el segon és l'expressió
a la dreta.
- A partir d'aquestes dues expressions, es defineix la funció
f(x, y) = y - ax - b, o bé
f(x) = x - a.
- La comanda avalua dóna el valor de
f(x, y) en el punt C. La icona
 pertany al menú
pertany al menú  i en aquest cas assigna un valor a les variables x i y.
i en aquest cas assigna un valor a les variables x i y.
Activeu la finestra, comproveu la interactivitat des del tauler gràfic
i valoreu la utilitat didàctica de l'activitat. |
| |
|
| |
|
 |
| |
|
| |
|