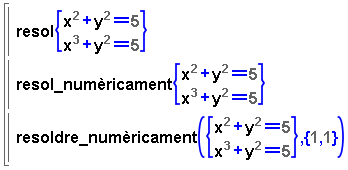|
|
Sistemes d'equacions |
| |
|
|
|
En aquesta pràctica, continuem el treball amb les comandes resol
i resol_numèricament aplicades a sistemes
d'equacions i donarem la visió gràfica quan sigui possible.
Veurem l'aplicació de mètodes numèrics a la resolució
de sistemes i comentarem la manera d'aprofitar les solucions d'un sistema,
tot aprofundint en l'estructura de llista de taules, és a dir la
manera com Wiris estructura les solucions.
Per la seva importància especial en els currículums de
la secundària els sistemes lineals es treballen a fons en la pràctica
següent com a aplicació dels recursos de l'àlgebra
lineal.
|
| |
|
| |
|
| |
Icona per escriure les equacions d'un sistema en la forma habitual: com
a llista vertical
|
| |
|
|
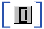
Escriure un sistema i obtenir-ne les solucions |
| |
|
|
|
- Les diverses equacions que componen el sistema que volem resoldre
s'han de passar, en forma de llista, com a arguments a la comanda que
interessi, resol o resol_numèricament.
- Per fer la presentació anàloga a la que és habitual,
es passa la llista d'equacions en forma vertical.
- Per escriure una llista vertical, teniu la icona
a la barra d'eines, que veureu fent clic a la pestanya  ,
acompanyada d'una finestra on podeu escriure el nombre d'equacions de
la llista.
- També teniu la possibilitat de fer clic a
 ,
a la barra d'eines, que us facilita la feina perquè escriu a
l'àrea de treball la comanda
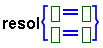
i ja teniu preparada la sintaxi amb els signes d'igual d'equació
amb què cal escriure les equacions. Feu clic a la primera casella
per entrar la primera part de la primera equació. Observeu que
les tecles del cursor us porten d'una casella a la següent. Si
ho feu així i voleu resoldre un sistema amb més de dues
equacions, necessitareu el menú de la barra d'eines per inserir-les:
|
|
Obriu la finestra activa de la Wiris (fent clic
a la icona de l'esquerra) i feu aquest exercici típic, que més
endavant reprendrem des del punt de vista gràfic: calculeu els punts
d'intersecció de les gràfiques de les funcions y = f(x)
i y = g(x) que podeu veure en la imatge següent: |
| |
|
| |
|
| |
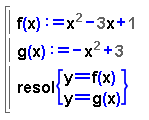
Definició de les fórmules i resolució d'un sistema
|
| |
|
|
|
- Completeu la finestra activa anterior seguint el model de la imatge.
- Recordeu que per accedir als exponents, podeu usar la combinació
de tecles
Control + Fletxa amunt.
- Executeu les comandes i observeu l'estructura de llistes en què
la Wiris ens retorna les solucions.
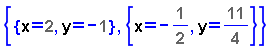
- Al final d'aquesta pràctica, veurem com extreure els valors
de les solucions d'aquesta estructura per poder-los assignar a variables
de memòria i emprar-los en càlculs posteriors.
|
|
|
Mètodes aproximats per resoldre sistemes |
| |
|
|
|
- Si resol respon { }(conjunt
buit) o bé nul, vol dir que,
per mètodes exactes no s'ha pogut trobar cap solució;
però pot ser que n'hi hagi.
- Els mètodes numèrics que incorpora la calculadora Wiris
també són aplicables per trobar una solució d'un
sistema d'equacions. La comanda resol_numèricament
selecciona el mètode més apropiat i intenta trobar una
solució a partir d'uns valors inicials.
- Si resol_numèricament respon {
} o bé nul, vol dir que el mètode emprat no ha
trobat cap solució. Si en troba, per a la Wiris només
n'hi haurà una.
|
| |
Obriu la finestra activa de la Wiris (fent clic
a la icona següent) i feu aquesta pràctica: |
| |
|
|
|
|
| |
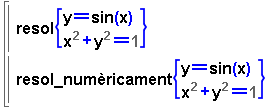
Comandes que trobareu en la finestra activa
|
| |
|
|
|
- Executeu les comandes de la finestra activa i observeu que la comanda
resol no troba cap solució; en canvi,
sí que n'obtenim una amb la comanda resol_numèricament.
- Entreu en el nou bloc de comandes que es crea després d'executar
el primer bloc i escriviu les comandes de la imatge següent, fent
servir la icona
per escriure'n la primera. Observeu com us podeu moure entre les diferents
parts del sistema amb les tecles del cursor. Per escriure la segona
comanda, podeu copiar i enganxar la primera (Control
+ c i Control + v) i després introduir el "_numèricament"
a mà.
- En la tercera comanda, observeu quina és la sintaxi per donar
un punt inicial on la Wiris comença
la recurrència i utilitzeu el teclat per entrar a mà la
comanda resol_numèricament (recordeu
que resoldre equival
a resol). Podeu
utilitzar la icona
per introduir els parèntesis i la icona
per introduir les equacions.
- Executeu aquest nou bloc de comandes i observeu les solucions obtingudes
en cada cas.
- Per acabar, deseu la finestra activa de la Wiris, usant la icona
de la pestanya 
i seguidament l'opció Anomena
i desa (o Guardar como )
del navegador.
|
| |
|
| |
|
| |
Aquestes són les comandes que heu d'introduir en la finestra activa
|
| |
|
|
|
L'estructura de les solucions
d'un sistema d'equacions |
| |
|
|
|
De la mateixa manera que per a les
equacions, la comanda resol retorna les solucions d'un sistema com
una llista de taules. |
| |
|
| |
- Cada una d'aquestes taules és una solució del sistema.
- En cada taula apareixen parelles xi=a per
a totes les xi variables de l'equació
o sistema i a el seu valor per a aquella solució.
Tot seguit se'n mostren exemples en una finestra activa i en el tema
següent, dedicat de manera explícita als sistemes d'equacions
lineals en veureu un exemple d'aplicació.
|
| |
|
|
|
Cliqueu a la icona de l'esquerra per veure dues
propostes diferents d'assignació a una variable de memòria
dels valors de les solucions d'un sistema, en una finestra activa de la
Wiris. Analitzeu i executeu el bloc de comandes i observeu els resultats
obtinguts. |
| |
|
| |
|
| |
Com assignar els valors de les solucions a variables de memòria
|
| |
|
|
|
- Recordeu que per escriure els subíndexs tenim la icona
de la pestanya També
es pot fer per teclat, amb Control + Fletxa
avall per entrar en el subíndex. Per sortir del subíndex,
podeu marcar la tecla Fletxa dreta.
|
| |
|
|
|
Representació gràfica de les
solucions d'un sistema de primer grau |
| |
|
| |
En aquest apartat veureu com representar les equacions i la solució
d'un sistema de primer grau. Aplicareu les idees que s'acaben d'explicar
sobre la manera d'obtenir les solucions del sistema. A partir de la llista
solució es defineix i dibuixa el punt solució del sistema.
En la finestra activa hi ha tres exemples:
- Si el sistema és determinat, s'escriu la solució,
es defineix i es dibuixa el punt solució.
- Si el sistema és indeterminat, la llista solució
expressa les dues incògnites en funció d'una d'elles i
no es representa cap punt solució.
- Si el sistema és incompatible, la llista solució
és buida, i el punt solució no queda definit.
En la finestra activa que s'obrirà en fer clic a l'icona de l'esquerra,
observeu els tres casos de sistema: compatible determinat,
compatible indeterminat i incompatible.
|
| |
|
|
|
| |
|
| |
- Fixeu-vos que es defineixen tres variables: sistema, sol
i S, que representen respectivament el sistema, la llista solució
i el punt solució.
- La comanda dibuixa que heu utilitzat per
dibuixar funcions, rectes i punts, en aquest cas té com a objecte
cadascuna de les equacions del sistema.
- La comanda escriu("Solució"|sol,punt(a,b))
escriu a partir del punt(a,b) del tauler gràfic,
el text entre cometes, i a continuació el valor de sol,
en aquest cas, la solució del sistema.
- Observeu, en els dos darrers casos, els missatges que apareixen en
la finestra inferior d'avisos.
|
| |
|
|
|
Posició relativa
de dues rectes |
| |
|
| |
En aquest exemple que heu de considerar d'ampliació en
una primera visió del tema però que, alhora, té una
interessant aplicació didàcyica:
- es defineixen dues rectes, cadascuna a partir de dos punts interactius
- es resol el sistema format per les dues rectes
- es determina el punt d'intersecció a partir de la solució
del sistema
- es representa gràficament la solució
|
| |
|
|
|
| |
|
| |
- Les comandes equació(r) i pendent(r)retornen
l'equació i el pendent, respectivament, de la recta r
definida geomètricament.
- En aquest cas, es visualitzen en el tauler gràfic les equacions
explícites de les dues rectes, les gràfiques i el punt
d'intersecció, si existeix.
- Observeu la interactivitat: en moure els punts A, B,
C i D es redefineixen les rectes i la solució del
sistema.
- Desplaceu els punts per observar els diferents casos de posició
entre dues rectes: es tallen en un punt paral·leles
i coincidents.
|
|
|
En l'exemple anterior haureu observat que en el tauler gràfic
s'escriu el valor del punt d'intersecció P assignat a partir
de la solució del sistema. Quan les rectes son paral·leles,
no retorna cap resposta, i quan el sistema és indeterminat, la
solució és una expressió de les incògnites
x i y en funció de y.
Per millorar les repostes de la Wiris i fer que escrigui explícitament
la paraula que explica quina és la posició relativa de les rectes (es
tallen, paral·leles, coincidents) quan es van movent els punts A,
B, C i D, convé afegir una mica de programació.
Això ens porta a allò que l'equip que redactem el curs en diem gràfics
amb resposta, que es tracten a bastament en la pràctica
4 del mòdul 4. Allà, també com a tema d'ampliació,
podeu completar aquest exemple.
|
| |
|
 |
| |
|
| |
|
