|
||||||||||||||||
| Pràctica |
|
|
|
Exercicis
|
||||||||||||
| Nombres complexos | |
|
Ja heu vist que la Wiris treballa amb nombres enters i racionals, opera amb aproximacions decimals dels nombres reals i també ho pot fer conceptualment amb valors exactes d'alguns nombres irracionals; finalment, ja heu vist algunes situacions on apareixen també nombres complexos. En aquesta pràctica veureu les possibilitats de treball amb nombres complexos: les operacions que hi podem fer, diferents funcions relacionades amb els nombres complexos i les presentacions que se'n poden fer, i, finalment, les possibilitats de representació gràfica que més endavant podreu aprofundir. |
|
 |
|
|
Icona de la unitat imaginària del menú
Anàlisi
|
|
|
|
Introducció de nombres complexos i operacions |
|
La unitat imaginària i
que es defineix com l'arrel quadrada de -1,
s'introdueix amb la icona Veurem de seguida com es poden efectuar les principals operacions: suma, producte, quocient i potències, i també constatarem el fet que es poden resoldre equacions polinòmiques amb coeficients complexos. Unes línies més avall teniu una foto d'una pantalla de treball amb la Wiris que podreu obrir efectivament si cliqueu a la icona de la fletxa. Us suggerim algunes exercitacions:
|
|
 |
|
|
Vegeu que la comanda resol que podem obtenir
amb la icona En canvi, si l'equació té coeficients reals, resol
no ens dóna per se les solucions en el domini complex. Recordeu
que vam veure de passada en la pràctica
3 del mòdul 1 que per trobar les solucions complexes d'una
equació polinòmica cal utilitzar la comanda arrels
especificant el conjunt |
|
|
|
Funcions complexes |
|
Les funcions més habituals relacionades amb el treball amb nombres complexos estan incorporades a la Wiris i no necessiten gaire explicació:
També tenim elements auxiliars de treball:
Podeu observar-ho si activeu la pantalla següent: practiqueu i investigueu. |
|
 |
|
|
|
Representació gràfica d'un nombre complex |
|
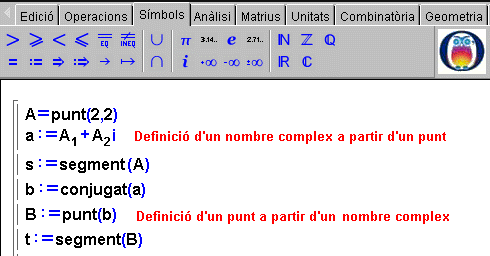
Com que la Wiris no té incorporat el dibuix d'un vector amb fletxa, que és el més usual quan es parla de representar gràficament els nombres complexos, se suggereix de representar-los mitjançant un punt que representi el que de vegades se'n diu l'afix i el segment que l'uneix amb l'origen de coordenades.
A la finestra activa podreu veure la representació d'un nombre complex i el seu conjugat. Observeu la interactivitat del gràfic. Com que aquesta acció només s'aconsegueix quan es mou un punt, s'ha de començar el codi definint un punt i fer servir el que s'ha explicat més amunt, la manera com a partir d'un punt del pla es defineix un nombre complex i a l'inrevés. Podeu analitzar amb detall el codi si activeu la finestra següent. |
|
 |
|
|
Algunes observacions sobre el codi de la pantalla activa que acabeu de veure:
|
|
|
|
Forma polar |
|
En aquesta part de la pràctica podreu comprovar un fet característic de la Wiris: una mateixa funció, segons els arguments que se li passin, pot servir per fer accions diferents. Observeu-ho en aquest cas, amb la comanda polar, que s'utilitza en el sentit de conversió de binòmica a polar i a l'inrevés.
|
|
 |
|
|
Ben segur que ja heu entrat a la finestra activa anterior i heu fet algunes investigacions. La darrera part us pot suggerir idees per un dels exercicis.
|
|
|
|
Representació polar |
|
|
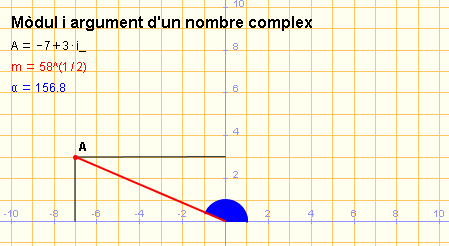
La finestra activa que presentem tot seguit fa visual de manera actualitzable/interactiva la representació en forma polar d'un nombre complex. En moure un punt del pla s'identifica amb el nombre complex que el té
per afix i es dibuixa el mòdul i l'argument, i se'n calculen i
es mostren els valors. Obriu la pantalla activa, feu l'activitat i observeu les diferències de presentació si hi ha la malla visible o no. |
 |
|
|
|
|
|
|
Suma de nombre complexos: la llei del paral·lelogram |
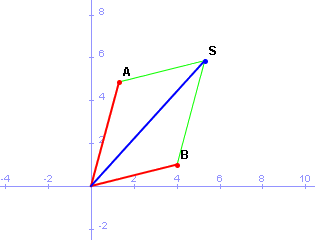
La interactivitat amb el tauler gràfic ens ha permès preparar una activitat d'orientació didàctica amb la finalitat d'observar les propietats geomètriques de la suma de nombres complexos. L'estructura d'espai vectorial de dimensió 2 dels nombres complexos fa que aquesta i d'altres representacions serveixin també per al treball amb els vectors del pla. |
|
 |
|
|
Representació gràfica de la suma de nombres
complexos
|
|
|
Si ja heu practicat amb aquesta activitat i n'heu mirat el codi, haureu pogut constatar, una vegada més, que una planificació clara i senzilla permet uns resultats excel·lents. A part d'altres aspectes que ja hem comentat anteriorment, en aquest cas volem fer notar una cosa que ben segur que ja heu experimentat: només hi pot haver una opció de color en cada comanda escriu o dibuixa. |
|
|
|
Arrels de nombres complexos |
|
Per trobar totes les arrels complexes d'un nombre real o bé d'un nombre complex, s'utilitza la comanda arrels, que rep dos arguments. Per calcular les arrels n-èsimes de r s'escriu arrels(r,n).
Tot seguit, es presenta una pantalla de la Wiris que, després
d'entrar un nombre complex r i un nombre natural n a la
finestra de sessió, es representen les arrels d'índex n
del nombre r a la circumferència de centre el punt (0,0)
i radi el mòdul de les arrels. |
|
 |
|
|
Activeu la finestra Wiris i veureu com es calculen i es mostren les arrels complexes. En primer lloc, us suggerim algunes idees per a petites modificacions.
Haureu d'analitzar el codi que en aquest cas presentem comentat i on trobareu un exemple molt interessant de la generació de llistes i el seu ús.
|
|
| Representació gràfica de les arrels d'un nombre complex | |
|
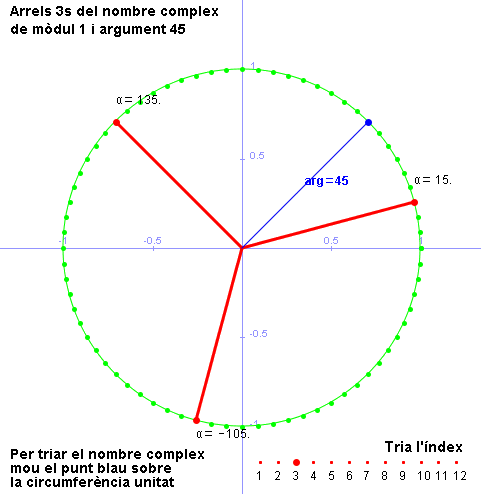
Tot seguit, presentem una nova activitat didàctica molt elaborada que permet explicar el mètode de càlcul de les arrels complexes d'un nombre complex en forma polar i fer-lo visual amb l'anàlisi de diferents exemples mitjançant la interactivitat dels gràfics de la Wiris. Es calculen i, sobretot, es presenten gràficament les arrels complexes d'un nombre complex de mòdul la unitat. Des del tauler gràfic s'escull el nombre complex i l'índex de l'arrel. Incloem aquí l'activitat, perquè creiem que il·lustra de manera excel·lent el tema que estem tractant, però hi ha molts aspectes que caldrà estudiar més a fons en altres mòduls.
Ara executeu l'aplicació que presentem. Ben segur que això
us motivarà per analitzar el codi quan sigui el moment i us donarà
idees per dissenyar les vostres pròpies activitats. |
|
 |
|
|
Representació gràfica de les arrels d'un
nombre complex
|
|