D112. Mòdul 2. Pràctica 5. La calculadora WIRIS com a recurs didàctic

Mòdul 2

La calculadora Wiris com a recurs didàctic

Pràctica

Exercicis

	Successions i progressions

	A partir de les propietats de les llistes i de les opcions lligades a la comanda progressió, veureu, en aquesta pràctica, com tractar les progressions i les successions en general i també com visualitzar termes d'una successió. En un darrer apartat trobareu un breu comentari sobre els signes de sumatoris i productes reiterats, que no apareixen en la majoria d'imatges de la calculadora Wiris perquè aquesta ha estat una novetat de la versió del programa establerta per al curs 2004-2005.

	Termes d'una successió

	Com heu vist en la pràctica 1 d'aquest mòdul, s'obtenen termes d'una successió a partir d'una llista. De forma molt senzilla si la succesió és una progressió aritmètica, i afegint el terme general o bé la llei de formació de la successió, mitjançant les comandes amb, en i on.



	Observeu tres formes diferents de trobar termes d'una successió de nombres. Canvieu el nombre d'elements, el terme general i la condició.

	Formes de definir una successió de nombres
	La Wiris permet definir una succesió de nombres de forma similar a com es defineix una funció, però restringint el domini al conjunt dels nombres naturals. De forma més conceptual, la Wiris permet introduir una successió amb la comanda comprovar, o bé amb les estructures de programació.



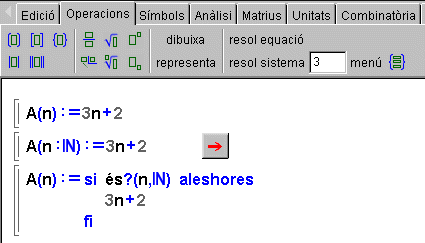
	Observeu les tres formes de definir la successió: en el primer cas, com una funció; en els altre dos casos, restringint el valor de n. En el segon cas, els dos punts de A(n:N)indiquen que n només pren valors en el conjunt del nombres naturals. No es pot utilitzar aquesta expressió per restingir valors a intervals. Més endavant, en la pràctica 1 del mòdul 6 dedicat a l'anàlisi, veureu com definir una funció definida a trossos. En el tercer cas, en la definició de la funció s'utilitza la sentència condicional si..aleshores..fi de la pestanya . Comproveu en cada cas la resposta de la Wiris quan n pren valors no naturals. Només en el primer dels casos permet calcular el límit de la successió.

	Representació gràfica de termes d'una successió

	Els termes d'una successió A(n) es representen en el tauler gràfic assignant a un conjunt de punts del pla els valors (n, A(n)) on n pren valors en el conjunt dels nombres naturals i A(n) representa el terme general de la successió.



	Observeu la forma de visualitzar els termes d'una successió: representació discreta mitjançant punts del pla i definits només per valors naturals, a diferència de la representació contínua de les funcions. La icona del menú permet calcular el límit de la successió i interpretar-ho gràficament. Amb la icona del tauler gràfic us podeu desplaçar per observar els termes de la successió. Canvieu la successió i observeu com varia el gràfic i s'actualitza el valor del límit.

	Progressions
	La Wiris incorpora mitjançant la comanda progressió la possibilitat d'estudiar una successió de nombres a partir dels seus primers termes, estableix el tipus de progressió i calcula l'expressió del terme general. La Wiris estableix el tipus de progressió de la forma següent: Si els termes formen part d'una successió constant, així ho indica. Si els termes que s'han donat poden formar part d'una progressió aritmètica, així ho indica. Si només es donen dos termes d'una successió, la tracta sempre com a progressió aritmètica. Si els termes de la successió no estan en progressió aritmètica ni constant, la Wiris estudia si es pot tractar d'una progressió geomètrica. Si no es tracta de cap de les situacions anteriors, la Wiris busca la successió polinòmica de grau més petit possible que s'ajusta a totes les dades donades. En general, per a tota successió finita de n nombres hi ha un polinomi de grau no superior a n -1 tal que els n primers termes de la successió polinòmica corresponent coincideixen amb els de la successió.



	Observeu com la Wiris determina el tipus de progressió. A la comanda progressió(x,y,z) canvieu els valors de x, y i z de forma que el resultat sigui: constant, aritmètica, geomètrica o bé polinòmica.

	Funcions associades a les progressions

	Una progressió es pot guardar en una variable, si p representa una progressió, p(i) retorna el terme i-èsim, p(n) el terme general. La comanda pas retorna la diferència de la progressió, si aquesta és aritmètica o constant. La comanda raó retorna la raó de la progressió, si aquesta és geomètrica o constant. Amb la comanda , del menú , es calcula el límit, si existeix, de la progressió.


	Demaneu el pas i la raó d'una progressió constant. Utilitzeu subíndexs perquè la Wiris retorni els termes generals de les progressions p i q de l'exemple.

	Suma dels termes d'una progressió

	Per calcular la suma dels termes d'una progressió s'utilitza la comanda sigma_progressió. La comanda té tres arguments: primer la progressió i després els límits inferior i superior del sumatori. Els límits del sumatori poden ser nombres enters, polinomis amb coeficients enters, o bé l'infinit.



	Calculeu la suma dels 100 primers termes d'una progressió aritmètica i d'una altra de geomètrica. En la darrera línia, observeu que la Wiris calcula el límit de la suma dels termes d'una progressió geomètrica de raó, en valor absolut, menor que la unitat.

	Noves icones en la versió de la Wiris per al curs 2004-2005

	Ben segur que ja us heu adonat que "les fotos" de l'entorn de treball de la calculadora Wiris que s'han inclòs fins ara en els materials del curs D112 no es corresponen amb la interfície de treball que veieu realment.

	Interfície de la Wiris del portal edu365 a partir del curs 2004-2005
	Els símbols de sumatori: Vegeu que es poden indicar els valors de la variable per als quals es vol efectuar la suma tant amb la formulació clàssica com fent servir els recorreguts de la Wiris. No s'incorpora la suma de sèries, és a dir, no es pot emprar el signe d'infinit. 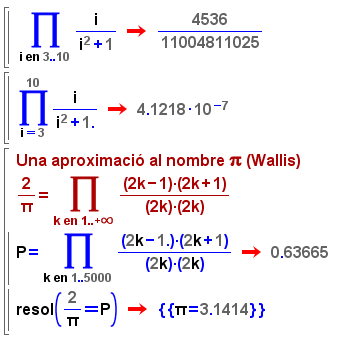(Vegeu també que en la darrera expressió p és el nom d'una variable, la lletra grega p; no s'ha fet, per tant, amb les icones de la pestanya , sinó amb les de .) Els símbols de productes múltiples, amb un exemple clàssic: Finalment, disposeu també d'icones per indicar les funcions part_entera i part_entera_superior, que podeu fer servir equivalentment a les comandes escrites: