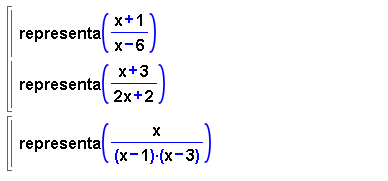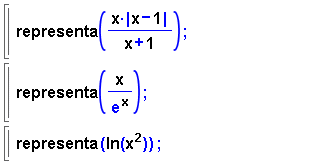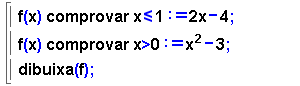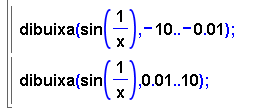|
|
Encara més sobre representació
gràfica de funcions |
| |
|
|
|
En la pràctica 5 del mòdul
1 heu vist les diferències entre  i
i  , i la potencialitat
didàctica d'aquesta darrera comanda. En la pràctica
1 del mòdul 3 s'han tractat diferents qüestions relatives
a la representació de funcions i el seu tractament formal. Reviseu,
si us cal, aquestes pràctiques. , i la potencialitat
didàctica d'aquesta darrera comanda. En la pràctica
1 del mòdul 3 s'han tractat diferents qüestions relatives
a la representació de funcions i el seu tractament formal. Reviseu,
si us cal, aquestes pràctiques.
En aquesta pràctica s'aprofundirà en el funcionament de
 ; també
veureu diferents qüestions pel que fa al tractament de funcions i
la seva representació gràfica. ; també
veureu diferents qüestions pel que fa al tractament de funcions i
la seva representació gràfica.
|
| |
|
|
|
La comanda representa |
| |
|
| |
La comanda està definida per a objectes del tipus funció
o bé cònica. La seva finalitat, com heu vist anteriorment,
és dibuixar aquests objectes i mostrar, a més, informació
rellevant.
Si s'aplica la comanda a un objecte per al qual la Wiris no té
definit com calcular cap element especial en la seva representació,
la comanda serà equivalent a  . .
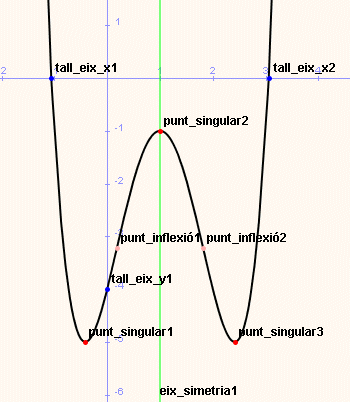
Pel que fa a les funcions, mostra:
- Els punts de tall amb els eixos de coordenades, de color blau.
- Els punts singulars, de color vermell.
- Els punts d'inflexió, de color rosa.
- Els punts en què la funció no és derivable,
de color rosa.
- Les asímptotes, de color blau.
- L'eix de simetria, de color verd.
- El punt de simetria central, de color verd.
La imatge següent mostra el nom de diferents elements de representació
d'una funció polinòmica. Ho podeu comprovar si activeu la
finestra Wiris i un cop feta la representació apropeu el ratolí
a cadascun d'ells, amb l'opció  del tauler gràfic activada.
del tauler gràfic activada.
|
|
|
|
|
|
|
| |
|
| |
- Activeu la icona
 del tauler gràfic i busqueu els valors de tots els elements que
es destaquen en la representació de la funció.
del tauler gràfic i busqueu els valors de tots els elements que
es destaquen en la representació de la funció.
- En el cas de funcions amb simetria central, mostra el centre de la
simetria que, en general, és un punt d'inflexió. En la
finestra gràfica observeu la coincidència dels dos punts
en les funcions del segon exemple.
- Hi ha molts elements que configuren una gràfica; en cas que
es vulgui fer alguna variació respecte al color o la mida cal
explicitar-ho.
|
| |
|
| |
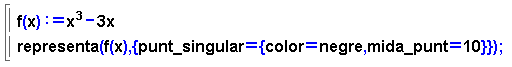
|
| |
|
| |
- En l'exemple anterior es canvia la mida i el color dels punts singulars
de la funció.
- Canvieu el color i el gruix de l'eix de simetria de la primera funció
de la finestra activa.
- En l'exercici 1 d'aquest mòdul
fareu servir aquesta opció per posar de manifest l'existència
de simetria en una funció.
|
| |
|
|
|
Modificacions del tauler gràfic |
| |
|
| |
Les comandes  i
i  trien les finestres
més adequades per presentar la gràfica de la funció.
No obstant això, tenim diferents opcions per modificar els taulers: trien les finestres
més adequades per presentar la gràfica de la funció.
No obstant això, tenim diferents opcions per modificar els taulers:
- Obrir un tauler nou sempre que convingui amb la comanda Tauler().
- Definir prèviament les mides del tauler, amb la comanda Tauler(P,x,y)
on P és el centre del tauler, x l'amplada, y
la llargada. Aquesta comanda només funciona amb l'opció
 . .
- Recuperar les característiques d'un tauler gràfic en
la sessió de treball, mitjançant la icona
 . .
Activeu la finestra i representeu les funcions que hi trobareu.
|
| |
|
|
|
|
| |
|
| |
- Per visualitzar millor i comparar les asímptotes de les dues
primeres funcions, afegiu entre elles la comanda
tauler().
- Per a la tercera funció, busqueu el tauler més idoni
per comprovar que un dels punts singulars de la funció és
un mínim local. Utilitzeu les icones
 i
i  del
tauler gràfic. del
tauler gràfic.
- Premeu la icona
 i observeu com els valors de la finestra gràfica es copien en
la finestra activa. Representeu de nou la funció amb aquests
atributs.
i observeu com els valors de la finestra gràfica es copien en
la finestra activa. Representeu de nou la funció amb aquests
atributs.
- Definiu un tauler centrat al punt (0,0) d'amplada i llargada 10 per
representar la darrera funció de la finestra. Utilitzeu l'opció
 . .
- En el tauler gràfic utilitzeu, quan convingui,
 per allunyar-vos i
per allunyar-vos i  per redibuixar la funció.
per redibuixar la funció.
|
| |
|
|
|
Asímptotes |
| |
|
| |
Un cop executada la comanda  ,
és possible recuperar els elements que ha presentat en la
representació gràfica: asímptotes, punts de tall,
punts singulars, etc. ,
és possible recuperar els elements que ha presentat en la
representació gràfica: asímptotes, punts de tall,
punts singulars, etc.
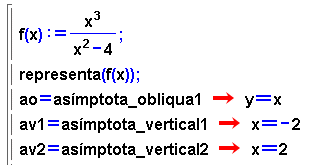
- En l'exemple següent veureu com es recuperen les expressions
de les asímptotes per escriure-les en el tauler.
- Tots els elements han de demanar-se amb la corresponent numeració,
tal com s'indica en la figura. Per això és millor mirar
primer la gràfica de la funció.
|
| |
|
|
|
|
| |
|
| |
- Els elements de representació poden utilitzar-se per a diferents
càlculs. Vegeu l'exercici 1 d'aquest
mòdul.
- En l'exemple següent es troba el punt d'intersecció d'una
funció amb la seva asímptota obliqua.
|
|
|

|
| |
|
| |
- Recordeu que les solucions d'un sistema format per dues funcions permeten
definir i dibuixar els punts d'intersecció entre les dues funcions.
- Busqueu la finestra més adient que mostri el punt d'intersecció
de la funció amb l'asímptota obliqua.
|
| |
|
| |
En algunes ocasions, us adonareu que la Wiris no indica les asímptotes,o
bé algun altre element especial de representació d'una funció.
En aquestes situacions, la comanda  és equivalent a
és equivalent a  . .
|
| |
|
|
|
|
| |
|
| |
- Representeu les funcions de la finestra activa i d'altres que se us
acudeixin. Fixeu-vos si es visualitzen o no en el tauler gràfic
els trets característics de la funció.
|
| |
|
|
|
Activitat sobre les asímptotes |
| |
|
|
|
Tot i que la comanda  ofereix moltes aplicacions didàctiques, no accepta alguns atributs
i és poc flexible. Per això, per preparar activitats és
preferible utilitzar la comanda
ofereix moltes aplicacions didàctiques, no accepta alguns atributs
i és poc flexible. Per això, per preparar activitats és
preferible utilitzar la comanda  . .
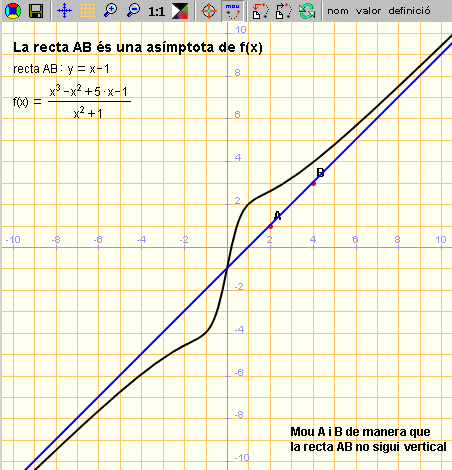
A continuació, veureu una activitat sobre les asímptotes
d'una funció. Consisteix a obtenir funcions que s'identifiquen
a l'infinit amb una recta; això s'aconsegueix de la forma següent:
f(x) = recta(r) + g(x), on g(x) tendeix a 0 en l'infinit.
- La funció f(x) té per asímptota la recta
r, que pot ser horitzontal o obliqua.
- El tipus de funció f(x) que s'estudia depèn de
g(x).
- Si g(x) és racional, f(x) també ho serà,
amb el numerador de grau igual o superior en una unitat al grau del
denominador, depenent de si la recta és de la forma y = a,
o bé
y = ax + b.
La finestra utilitza diferents recursos de la Wiris:
- Definició de dos punts mòbils, A i B,
en el tauler gràfic i obtenció de la recta r que
determinen.
- Actualització de la recta r en moure els punts A
i B, i d'una funció f(x) que té la recta
per asímptota.
- Definició de diferents tipus de funció f(x),
a partir d'una altra funció g(x) que es modifica des de
la pantalla activa de la Wiris.
- Extracció mitjançant subíndexs dels elements
d'un objecte; en aquest cas, del segon terme de l'equació de
la recta.
- Presentació en el tauler gràfic d'informació
que s'actualitza en moure els punts A i B; en l'exemple,
les equacions de la funció i l'asímptota, horitzontal
o obliqua.
|
|
|
|
| |
|
| |
La interactivitat de la finestra, acompanyada de les instruccions i indicacions
pertinents, serveix als alumnes de secundària per:
- Assolir el concepte de recta a la qual tendeix una funció a
l'infinit, és a dir, el concepte d'asímptota horitzontal
o obliqua, per un costat, per l'altre o per ambdós.
- Consolidar el concepte de límit d'una funció a l'infinit.
- Generar diferents tipus de funcions que tenen una asímptota
obliqua, a partir d'una funció que tendeix a 0 en l'infinit.
- Deduir la condició que han de verificar les funcions racionals
per tenir una asímptota horitzontal o bé una d'obliqua.
- Calcular de forma ràpida les asímptotes horitzontals,
o bé el pendent i l'ordenada a l'origen de l'asímptota
obliqua, en els cas de les funcions racionals.
L'activitat també es pot orientar cap a l'obtenció de l'equació
de l'asímptota a partir de la divisió entera entre numerador
i denominador, en el cas de funcions racionals.
|
| |
|
|
|
|
| |
|
|
|
Discontinuïtats i punts de no-derivabilitat |
| |
|
| |
- La comanda
 indica, en alguns casos, en el tauler gràfic els punts en què
la funció no és contínua o bé no és
derivable. En d'altres casos, com és ara el de funcions exponencials,
logarítmiques o bé trigonomètriques, no calcula
res i equival a
indica, en alguns casos, en el tauler gràfic els punts en què
la funció no és contínua o bé no és
derivable. En d'altres casos, com és ara el de funcions exponencials,
logarítmiques o bé trigonomètriques, no calcula
res i equival a  . .
- Mitjançant discontinuïtats(f)
es calculen els punts en què la funció f no és
contínua. Aquesta comanda detecta punts de discontinuïtat
que l'opció
 no considera.
no considera.
- En la finestra trobareu diferents exemples de funcions amb punts de
discontinuïtat, o bé amb punts en què la funció
no és derivable.
|
| |
|
|
|
|
| |
|
| |
- Representeu les funcions que apareixen en la finestra i compareu-ho
amb el resultat de la comanda discontinuïtats.
- La Wiris presenta problemes per a la representació de la la
funció sin(1/x): només es pot dibuixar eludint
el punt (0,0). Al final de l'apartat següent trobareu una forma
de dibuixar-la.
|
|
|
|
|
|
Funcions definides a trossos |
| |
|
| |
- Per dibuixar una funció definida a trossos s'utilitza
la comanda dibuixa(f,a,b) o bé dibuixa(f,a..b)
, que restringeix la gràfica de la funció f a l'interval
[a, b].
- Per definir una funció definida a trossos cal utilitzar
les opcions de programació: el condicional si..aleshores..altrament..fi
|
| |
|
|
|
|
| |
|
| |
- Una altra forma de definir una funció definida a trossos és
amb l'operador comprovar.
- En ambdós casos, les funcions estan ben definides. Per comprovar-ho
busqueu les imatges d'alguns punts.
|
| |
|
| |
|
| |
|
| |
- Una forma de representar la funció sin(1/x) és
restringir-la als intervals: (-10,-0.01) i (0.01,10). D'aquesta manera,
s'evita el punt (0,0) en què la funció no té límit.
|
| |
|
| |
|
| |
|
| |
|
 |
| |
|
| |
|