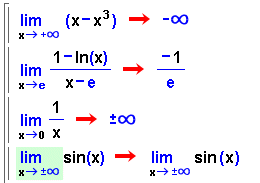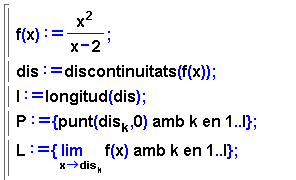| |
Càlcul de límits |
|
|
|
| |
En aquesta darrera pràctica del mòdul
6 dedicat a l'anàlisi es tracta el càlcul de límits,
per això analitzeu primer les icones del menú  relatives al càlcul de límits: una per al límit central,
i dues per als límits laterals, de dreta i esquerra.
relatives al càlcul de límits: una per al límit central,
i dues per als límits laterals, de dreta i esquerra. |
| |
|
| |
|
| |
Icones relatives al càlcul de límits del
menú Anàlisi
|
| |
|
| |
Del menú  utilitzarem els signes de més infinit, menys infinit i amb el doble
signe que equival a l'infinit sense signe.
utilitzarem els signes de més infinit, menys infinit i amb el doble
signe que equival a l'infinit sense signe. |
| |
|
| |
|
| |
Icones de l'infinit al menú Símbols
|
| |
|
|
|
Límit central |
| |
|
|
|
- En fer clic sobre la icona
 ,
apareixen tres capses buides de color verd. A la capsa superior es col·loca
l'expressió o funció de la qual es calcula
el límit. En les capses inferiors, a l'esquerra de la fletxa
es posa la variable del límit i a la dreta el límit
al qual es fa tendir la variable. ,
apareixen tres capses buides de color verd. A la capsa superior es col·loca
l'expressió o funció de la qual es calcula
el límit. En les capses inferiors, a l'esquerra de la fletxa
es posa la variable del límit i a la dreta el límit
al qual es fa tendir la variable.
- De forma equivalent, per calcular el límit de la funció
f quan x tendeix a a, es poden fer servir les expressions
límit(f,x,a) o límit(f,x
 a).
La icona de la fletxa es troba al menú a).
La icona de la fletxa es troba al menú  . .
- El valor de a pot ser un nombre real, una expressió
o qualsevol de les tres icones de l'infinit.
|
| |
|
| |
|
| |
|
| |
- En alguns casos, cal posar l'expressió entre parèntesis.
Fixeu-vos què passa si traieu els parèntesis del primer
exemple de la finestra.
- Observeu que si els límits per la dreta i per l'esquerra són
diferents, o si no hi ha límit, apareix un missatge a la finestra
d'errors.
- Si el límit és més infinit per un costat i menys
infinit per l'altre, el resultat és
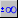 . .
- El càlcul de límits no es pot aplicar a les funcions
definides a trossos.
|
| |
|
|
|
Límits laterals |
| |
|
|
|
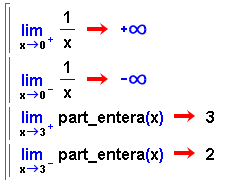
- Les icones
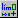 i
i  permeten
fer els límits laterals per la dreta i per l'esquerra
respectivament. La sintaxi de les comandes és la mateixa que
l'anterior. permeten
fer els límits laterals per la dreta i per l'esquerra
respectivament. La sintaxi de les comandes és la mateixa que
l'anterior.
- Igual que l'apartat anterior, per calcular el límit de la funció
f quan x tendeix a a per la dreta, es poden fer
servir les expressions límit(f,x,a,1)
o límit(f,x
 a,1).
a,1).
- Per l'esquerra les expressions són límit(f,x,a,-1)
o límit(f,x
 a,-1).
a,-1).
|
| |
|
| |
|
| |
|
| |
- A la finestra trobareu diversos exemples, feu les proves que considereu
pertinents i comproveu l'efectivitat dels càlculs.
|
| |
|
|
|
Domini, discontinuïtats i límits |
| |
|
|
|
El següent grup de comandes permet estudiar el concepte de domini
d'una funció i veure el comportament en els punts de discontinuïtat.
S'utilitzen les comandes següents:
- domini(f(x)) calcula el domini de
la funció f(x). El resultat és un conjunt de nombres
expressat en forma de condició o com a conjunt de nombres.
- discontinuïtats(f(x)) calcula els valors
de x en què f presenta algun tipus de discontinuïtat.
- També es calculen els límits en els punts de
discontinuïtat i es dibuixa la funció.
|
| |
|
| |
|
| |
|
| |
- La Wiris no considera el tipus de discontinuïtat que es pot evitar
simplificant l'expressió de la funció. A la finestra Wiris,
fixeu-vos en el segon exemple.
- Proveu la resposta de la Wiris davant altres tipus de discontinuïtats.
|
| |
|
|
|
Gràfica, domini, discontinuïtats
i límits |
| |
|
|
|
A partir del grup de comandes anterior, es prepara una activitat que
presenta en el tauler gràfic la gràfica de la funció,
el seu domini, els punts de discontinuïtat i el límit
de la funció en aquests punts.
Aquesta activitat serveix per relacionar els conceptes que hi apareixen,
tot fent servir la representació gràfica i la possibilitat
de l'estudi de diferents funcions que es poden canviar des de la finestra
Wiris.
Cal vigilar la resposta per a algunes funcions, com les que tenen infinits
punts de discontinuïtat, i les que presenten salts.
|
| |
|
| |
|
| |
|
| |
- La variable dis és una llista que conté tots
els valors de x en què la funció és discontínua.
- La longitud de dis l'anomenem l, i representa el nombre
de punts de discontinuïtat.
- P és la llista formada pels punts d'abscissa x,
f discontínua en x, i ordenada 0.
- L és la llista que conté els límits de
f en els punts de discontinuïtat.
- Després d'aquestes comandes, s'afegeixen les d'escriptura i
dibuix.
|
| |
|
| |
|
| |
|
|
|
- Obriu la finestra Wiris i avalueu les possibilitats didàctiques
de l'activitat.
- Feu algun canvi en l'activitat, com per exemple canviar en els punts
de discontinuïtat els límits centrals pels laterals.
|
| |
|
| |
|
 |
| |
|
| |
|