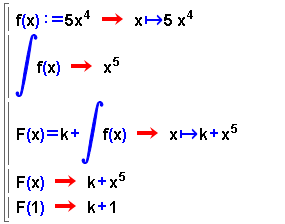D112. Mòdul 6. Pràctica 4. La calculadora WIRIS com a recurs didàctic

Mòdul 6

La calculadora Wiris com a recurs didàctic

Pràctica

Exercicis

	Càlcul de primitives i integral definida

	El procés invers a la derivació d'una funció és el que es coneix com el càlcul de primitives, la funció resultant s'anomena primitiva o integral indefinida.


	Icones relatives al càlcul integral del menú Anàlisi

	Primitiva d'una funció

	La Wiris calcula la primitiva d'una expressió algebraica o d'una funció definida prèviament mitjançant una de les formes següents: La icona (Primitiva) del menú . En fer clic a la icona, apareixen dues capses buides; en la de més a l'esquerra entre el símbol d'integral i la d del diferencial, s'escriu l'expressió o funció que es vulgui integrar i a l'altra capsa s'escriu la variable respecte a la qual es vulgui integrar. El resultat és sempre una expressió. Si no hi ha dubte sobre la variable respecte de la qual es vol integrar, es pot utilitzar també la icona (Primitiva d'una funció). En aquest cas, apareix una sola capsa buida on s'escriu l'expressió o funció que s'ha d'integrar. El resultat és una expressió o una funció segons quin sigui l'argument introduït; interpreta una funció quan s'escriu solament la lletra assignada a una funció. Alternativament, també s'utilitza la comanda integra amb un argument: integra(expressió o funció) o dos: integra(expressió o funció,variable) segons si cal precisar la variable respecte a la qual s'integra. Si s'utilitza la comanda integra amb un sol argument o bé la icona i l'expressió no té variables, la Wiris integra respecte a una variable inventada, si té una única variable integra respecte a aquesta, i si en té més d'una no fa res.



	Observeu diferents formes de càlcul de primitives; en la imatge anterior l'objecte resultant és una expressió algebraica. Obriu la finestra de la Wiris d'aquest apartat i observeu els exemples en què el resultat és una expressió i els que és una funció. Per definir una funció s'utilitza := o bé la icona . La Wiris retorna la variable i l'expressió de la funció separades per ; aquesta icona, que és al menú , els autors l'anomenen Constructor de funcions pures. En la imatge següent l'objecte resultant de la integral és una funció.



	Integral indefinida

	En l'apartat anterior heu vist que la Wiris calcula una primitiva, però no apareix la constant d'integració, que s'acostuma a posar en el càlcul de primitives. Perquè quedi definit el conjunt de totes les primitives, que s'anomena integral indefinida, cal afegir la constant d'integració. Es pot definir la integral indefinida F(x) a partir de l'expressió d'una primitiva i sumant una constant. En aquest cas, cal utilitzar el signe = per definir la funció F(x).



	Un exemple d'aplicació del càlcul anterior: trobar la funció que passa pel punt (2, 3) i té per derivada la funció g(x) = 3x²- 10x. En la finestra de la Wiris trobareu el resultat. De forma similar, i després d'haver vist en el proper apartat la sintaxi de càlcul de la integral definida, resoleu l'exercici 4 d'aquest mòdul.

	Integral definida

	La Wiris calcula la integral definida entre dos valors mitjançant una de les formes següents: La icona del menú . En fer clic a la icona, apareixen quatre capses buides per introduir els límits d'integració, la funció o expressió, i la variable respecte a la qual s'integra. Aquesta opció és la que es recomana. La icona s'utilitza si no hi ha dubte de la variable respecte a la qual s'integra; en aquest cas apareixen tres capses buides. La comanda integra amb quatre arguments: l'expressió, la variable, el límit superior i el límit inferior. Es pot prescindir d'indicar la variable. La Wiris intenta calcular la primitiva i després aplica la regla de Barrow; si no troba primitiva, fa el càlcul de la integral definida amb mètodes numèrics.



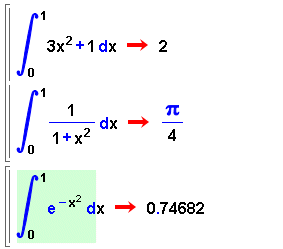
	Obriu la finestra de la Wiris i observeu que en el cas que la Wiris utilitzi mètodes numèrics apareix una indicació gràfica (requadre verd) a la pantalla i un missatge a la finestra d'errors. No calen parèntesis, però es poden posar per facilitar la comprensió de l'expressió integral.

	Integrals impròpies

	La Wiris incorpora la possibilitat de càlcul d'integrals impròpies. Tant en el cas que alguns dels límits d'integració siguin infinits com en el cas que l'interval d'integració presenta alguna discontinuïtat.



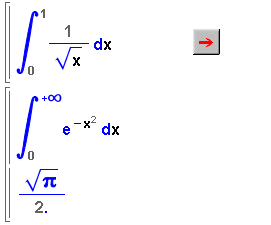
	La Wiris calcula només algunes integrals impròpies; vegeu els exemples de la finestra i feu més proves. A la imatge, una integral impròpia que la Wiris calcula de forma aproximada; compareu-ho amb el resultat exacte posat a continuació de la integral. Llegiu els missatges a la finestra d'errors.