D112. Mòdul 6. Pràctica 2. La calculadora WIRIS com a recurs didàctic

Mòdul 6

La calculadora Wiris com a recurs didàctic

Pràctica

Exercicis

	La derivada amb la Wiris

	El càlcul diferencial és un dels temes central en l'anàlisi matemàtica. Les opcions de càlcul simbòlic en relació amb el càlcul diferencial permeten, de forma senzilla, fer càlculs, resoldre exercicis i comprovar resultats. A partir de la representació gràfica i aprofitant la interactivitat de les finestres gràfiques, es poden preparar activitats dirigides als alumnes de secundària sobre qüestions relatives al concepte de derivada i les seves aplicacions, com és ara: la definició de recta tangent, el concepte de funció derivada, la relació entre el signe de la derivada i el creixement d'una funció, etc. Tot seguit, us mostrem una animació feta amb el programa Flash-Cam a partir de la captura de pantalles de la Wiris que mostra de manera dinàmica el concepte de recta tangent com a límit de la posició de rectes secants. En el context de la pràctica escriureu el codi de la Wiris que permet fer aquesta activitat.


	La tangent (recta vermella) com a límit de les secants (rectes verdes)

	Diferents formes d'expressar la derivada

	La Wiris calcula la derivada d'una expressió o d'una funció mitjançant una de les formes següents: La comanda deriva. Si l'expressió té més d'una variable, cal indicar la variable respecte a la qual es deriva deriva(expressió,x). La icona del menú Anàlisi. En aquest cas, apareixen dues capses buides; a la superior s'escriu l'expressió que es vol derivar, i a l'inferior, la variable respecte a la qual es deriva. No necessita parèntesis. L'apòstrof ' està col·locat darrere de l'expressió que es vol derivar. Si l'operador ' s'aplica a una expressió de més de dues variables, no fa res. Per funcions admet dues posicions: f(x)' i f'(x). Si f(x) és una funció i a és un nombre real, l'expressió f'(a) correspon al valor numèric de la derivada en a.



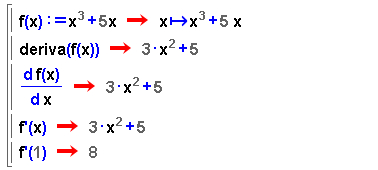	Comproveu en la finestra activa les diferents opcions de sintaxi per calcular funcions derivades de funcions definides prèviament o d'expressions, així com per calcular derivades numèriques.

	La recta tangent com a límit de rectes secants

	La recta tangent a una funció en un punt es defineix com la posició límit de rectes secants. Ben segur que us serà familiar el dibuix de diferents rectes secants que es van apropant a la recta tangent; n'heu pogut veure un exemple dinàmic com a presentació d'aquesta pràctica, però ara us proposem que elaboreu l'activitat i vegeu que la interactivitat que s'aconsegueix a mà és també excel·lent En la finestra següent es dibuixa una funció, un punt sobre la funció i la seva recta tangent. Es defineix un punt mòbil per a l'eix d'abscisses i es dibuixa la recta secant determinada pel punt de tangència i pel punt imatge del punt mòbil. Observeu els passos que s'han de seguir: Representar una funció f(x) i un punt P sobre la funció. El punt P és la imatge a la gràfica de la funció d'un punt P1 que es mou per l'eix d'abscisses. Utilitzant la comanda punt_més_proper s'imposa que P1 es mogui per l'eix d'abscisses i llavors es fa que P sigui la imatge de P1 i, per tant, es mourà per la gràfica de la funció. Es pot fer de seguida una prova de dibuix.



	L'execució d'una prova de dibuix pot servir per buscar la millor finestra que mostri de manera adequada el gràfic que volem fer: Amb les icones del tauler gràfic es por buscar la mida adequada. Clicant a es pot moure la figura fins que quedi en la posició que interessi. En aquest cas, convé que no aparegui la malla per poder moure lliurement el punt P1 i és més clara la presentació sense cap informació per defecte depenent del moviment del ratolí (a part de la que s'escriu voluntàriament): i . Quan la presentació sigui l'adequada, es pot clicar a la icona i s'escriuen en la finestra de comandes les instruccions que defineixen els atributs del tauler. No confongueu aquesta icona amb , que serveix per tornar a la situació inicial després d'haver mogut punts del gràfic amb el ratolí. Després, convé clicar a perquè el gràfic torni a ser interactiu. Encara que les icones són prou explícites, consulteu, sempre que us convingui, la taula d'accions de totes les icones de la Wiris. Trobareu quelcom semblant al que podeu veure en les línies següents:


	A continuació es poden definir: La recta tangent a la funció f(x) en el punt P. Si es treballa amb les referències dels punts en lloc de valors concrets, permet fàcilment repetir l'exemple per un altre punt de tangència. Un punt A que es mogui per l'eix d'abscisses i el punt B imatge de A a la funció. La recta secant per P i B.


	Ja només queden per definir, si us fixeu en la il·lustració que es mostra al principi de la pràctica: Els segments auxiliars de la gràfica. Alguns d'aquests segments auxiliars són segments de punts que es defineixen mitjançant llistes de punts (k i j en les línies següents).


	I llavors, s'ha d'acabar amb les comandes de dibuix de la funció, rectes, segments i punts, en diferents colors i mides. Tot seguit, en teniu un exemple, però vosaltres podeu fer la vostra pròpia presentació personalitzada.


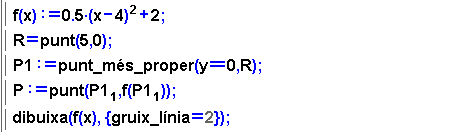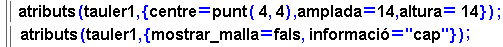	Proveu d'escriure l'activitat a partir de les indicacions que s'han anat donant. De tota manera, en trobareu una possible versió ja resolta si cliqueu a la icona de l'esquerra. Hi trobareu que, en funció de les característiques concretes del tauler, s'han inclòs unes explicacions per a la interactivitat. I si ara es vol fer la presentació amb una altra funció? Només caldrà canviar-la a la primera línia; es podrà fer a mà com ja s'ha indicat la definició de les millors característiques del tauler i, això sí, si es canvien aquestes característiques (que llavors quedaran escrites al final de les línies de codi), també caldrà canviar la posició dels rètols i les indicacions.

	La funció derivada a partir del pendent de rectes tangents

	La posició de la recta tangent a una funció en un punt es pot presentar com la posició que tindria un vagó que circulés per la funció com si es tractés d'una muntanya russa. Aquesta simulació es presenta en l'activitat següent. Es visualitza la posició de la recta tangent i el valor del pendent d'aquesta recta en diferents punts de la funció, mitjançant un punt mòbil de la funció, és a dir, un punt que recorre la funció. Les comandes següents calculen l'equació de la recta tangent t(x) a una funció f(x) en un punt A. L'abscissa del punt queda definida per un punt P que es mou per l'eix d'abscisses, mitjançant la comanda punt_més_proper(recta,punt). Es calcula també el pendent m de la recta tangent i es defineix el segment determinat pels punts P i A.



	Les comandes següents d'escriptura i dibuix, a més de representar la funció i la recta tangent en un punt, mostren les coordenades del punt i el pendent de la recta tangent. Els valors del tauler gràfic s'actualitzen en moure el punt. En la comanda escriu hi ha text entre cometes i noms de variables; per encadenar s'utilitza el connector \|.



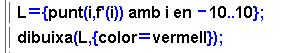	La funció derivada d'una funció es defineix com la que a cada valor i assigna el pendent de la recta tangent en el punt imatge, és a dir f'(i). Si es construeix una taula amb diferents valors i per l'abscissa, f'(i) per ordenada i es representen aquests punts, s'obté un esbós de la gràfica de la funció derivada. Les comandes següents defineixen i dibuixen una llista L de punts, amb valors de l'abscissa de -10 a 10, i el pendent o derivada per valors de l'ordenada.



	En l'activitat que s'obre amb la icona de l'esquerra veureu que per comprovar com es defineix la funció derivada es presenten en un mateix tauler la gràfica de f i diferents punts de la gràfica de la funció derivada f'. Afegiu algun comentari més al tauler. Vegeu l'exercici 2 d'aquest mòdul on us demanem que presenteu un estudi d'aquest tema. Per il·lustrar i acabar la pràctica, s'inclou una animació (feta amb el programa Flash-Cam, no solament amb la Wiris!) que presenta la línia de treball fonamental de l'activitat que s'acaba de mostrar.


	Podeu experimentar amb diverses posicions de la tangent