Entreu a la pàgina web citada, observeu que es compon de cinc unitats didàctiques, de les quals el producte escalar, és l'última, i que hi ha un manual de l'aplicació.

Menú inicial de les Activitats sobre vectors en el pla

Al manual de l'aplicació trobareu una descripció de l'aplicació, guies tant per al professorat com per a l'alumnat, i activitats d'avaluació. Un petit resum del manual és:

• Activitats sobre vectors en el pla és un recurs educatiu de 50 activitats estructurades en 5 unitats didàctiques, organitzades en forma de conjunt de pàgines web i que pot ser utilitzat tant en línia (connectat a Internet) com en forma local (sense connexió).
• És un material pont entre l'ESO i el batxillerat, ja que, en part, és utilitzable a 4t curs d'ESO (per exemple, en un crèdit o itinerari per als alumnes amb intencions de cursar un batxillerat científicotecnològic), i tot el material es pot fer servir al propi batxillerat científicotecnològic (aleshores les primeres unitats didàctiques constituiran un repàs).
• L'objectiu respectiu de cada unitat didàctica és:
     1) Treballar amb vectors donats gràficament (fletxes).
     2) Treballar amb vectors utilitzant coordenades i components.
     3) Treballar amb mòduls i arguments (vectors en forma polar).
     4) Aplicar els vectors per resoldre problemes de geometria plana.
     5) Introduir el producte escalar de dos vectors i fer-ne algunes aplicacions.
• Cada unitat té 10 activitats i cada activitat, la mateixa estructura: una petita explicació, una activitat interactiva i una proposta de treball.
  

Exploreu el conjunt d'activitats i consulteu el manual per completar el coneixement d'aquest recurs.

Cada activitat consta de tres parts:

• Una petita explicació (1 a la figura).
  En ella s'introdueixen conceptes i/o s'expliquen determinats procediments (d'una forma resumida).
• Una activitat interactiva (2).
  Aquestes activitats interactives inclouen un applet fet amb el programari de geometria interactiva Cinderella.
• Una proposta de treball (3).
  Són treballs de consolidació dels conceptes/procediments adquirits en l'activitat.

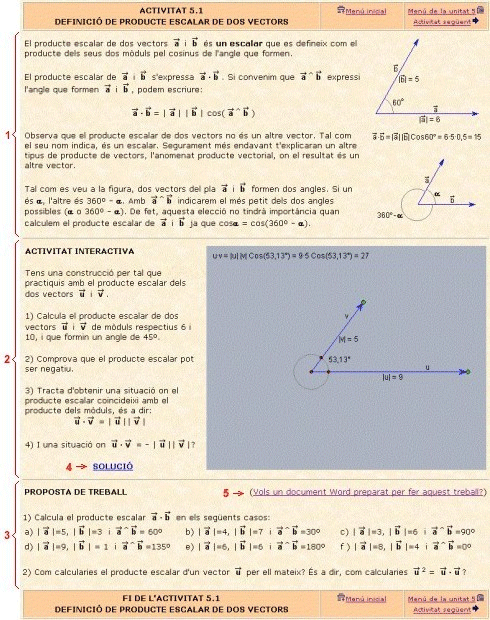
Definició de producte escalar de dos vectors

Els alumnes han de:

• Llegir amb atenció les explicacions (1).
• Fer les activitats interactives (2).
  Generalment, la realització de l'activitat exigeix polsar amb el botó esquerre del ratolí sobre certs punts (punts verds), desplaçar-los mantenint el botó polsat i obtenir determinats resultats.
  S'ha de defugir exigir excessiu perfeccionisme als resultats. Per exemple, si en comprovar una determinada propietat, l'alumne/a no encerta a posar el punt exactament al lloc on correspon, però fa una construcció que de forma aproximada mostra que la propietat es verifica, s'haurà de donar per feta la comprovació.
  Totes les activitats interactives van acompanyades d'un enllaç (4) que dóna la solució corresponent. El professor/a ha de controlar que els alumnes facin les activitats interactives, que no es limitin a consultar els resultats ni es precipitin a veure'ls.
• Fer les propostes de treball (3).
  Ho poden fer a la seva llibreta o quadern de treball, o bé utilitzant documentsplantilla Word (5) preparats per fer la proposta de treball corresponent, i que es poden imprimir.
  Aquesta feina la poden fer a classe o a casa, però s'aconsella que la comencin a fer a classe i l'acabin a casa si no l'han poguda acabar a classe (són el que sempre s'han anomenat deures).

3) La unitat 5: Producte escalar de dos vectors

Si ens centrem ara en aquesta unitat, tenim que els seus objectius són:

1. Fer el producte escalar de dos vectors geomètricament. A l'activitat 5.1 s'introdueix el producte escalar com a producte dels seus mòduls pel cosinus de l'angle que formen.

2. Interpretar geomètricament el producte escalar. A l'activitat 5.2 s'interpreta com el producte del mòdul d'un d'ells per a la projecció de l'altre sobre ell.

3. Estudiar les propietats commutativa, associativa respecte dels escalars, i distributiva del producte escalar, cosa que es fa a les activitats 5.3 i 5.4.

4. Fer el producte escalar de vectors treballant amb components. A l'activitat 5.5 s'obté la fórmula 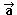·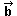= (a₁,a₂)·(b₁,b₂) = a₁b₁+ a₂b₂.

5. Identificar vectors perpendiculars i verificar condicions de perpendicularitat de vectors. A l'activitat 5.6 es defineixen, de forma raonada, vectors perpendiculars com a vectors amb producte escalar zero.

6. Obtenir el cosinus de l'angle que formen dos vectors i l'angle que formen dos vectors, cosa que es fa a l'activitat 5.7.

7. Projectar un vector sobre un altre, operació que es treballa fa a l'activitat 5.8.

8. Aplicar el producte escalar per demostrar alguns teoremes clàssics de geometria plana, cosa que es fa a les activitats 5.9 (un teorema molt conegut i atribuït a Tales) i 5.10 (el teorema de Pitàgoras).