|
||||||||||||||||
| Pràctica |
|
|
|
Exercicis
|
||||||||||||
|
|
Geometria analítica de l'espai |
|
|
|
|
En la pràctica 2 del mòdul 4 ja vam donar unes idees bàsiques dels recursos de què disposem amb la Wiris pel que fa a la geometria de l'espai. En concret vam veure la construcció de determinades figures i vam reflexionar sobre la forma de presentar els gràfics en tres dimensions. En aquesta pràctica continuarem amb l'estudi de la geometria de l'espai però ara posarem l'èmfasi en l'enfocament que hi dóna la geometria analítica. Un tema, doncs, que enllaça amb els continguts del darrer curs del batxillerat i que no es pot considerar, en absolut, imprescindible per al bon seguiment del curs D112. |
|
| Geometria analítica de l'espai i visualització amb la Wiris | |
|
Convé que investigueu (o que consulteu al manual) l'acció
de les icones disponibles a la carpeta
És important reprendre la reflexió sobre la manera de presnetar els gràfics en la Wiris. Recordem-ho: "només allò que es veu dintre del cub de representació". Repetim una idea que ja hem donat en el mòdul 4. Oi que a la pissarra
quan heu de representar un pla ho feu així: |
|
|
En canvi ja hem vist que la Wiris pot mostrar un pla de maneres ben diferents. Per exemple aquestes:
Tres aspectes que ens pot oferir la representació d'un pla
|
|
|
Per mostrar dos plans paral·lels o tres plans que es tallen en una recta sovint es fa així:
Tanmateix la necessitat inherent a un programa informàtic de realitzar els gràfics 3D seguint el rigor de la perspectiva i d'assenyalar un element referencial (ja s'ha comentat que els autors de la Wiris han triat un cub) pot fer que no se'ns mostri tan intuïtivament. Vegeu-ho:
Dos punts de vista diferents dels plans x+2y+z=20 i x+2y+z=30
Dos punts de vista diferents de tres
plans que es tallen en una recta,
|
|
|
Després d'aquestes reflexions que caldrà tenir ben presents sempre que es facin dibuixos de rectes i plans passem a veure com cal treballar en la geometria analítica. Adjuntem exemples en una finestra activa que podeu obrir, com és habitual, amb la icona de l'esquerra. Entre altres objectius, un dels que esperem aconseguir és incitar
els lectors i les lectores a consultar adequadament la Guia Ràpida
i l'Índex Alfabètic (les dues parts del Manual
del programa). Tanmateix potser trobareu a faltar algunes explicacions
en el manual i per això, tot seguit, comentem alguns aspectes del
codi de la finestra activa anterior centrant-nos en les idees analítiques
i la utilitat (i alguna anomalía) de les icones de la carpeta |
|
| En el primer bloc de comandes es calcula la recta R perpendicular a un pla P que passa per un punt donat, A. | |
 |
|
|
|
| En l'últim bloc de comandes es resol un
problema en certa manera invers a l'anterior. Prenent com a dada la recta
R (la solució d'abans) calcular el pla |
|
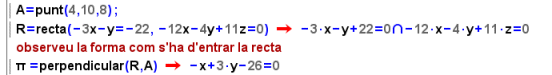 |
|
|
|
|
Hem pogut observar que la mateixa comanda perpendicular(figura,punt) ens ha servit per obtenir la recta perpendicular a un pla i el pla perpendicular a una recta.
|
|
| Més comandes per a rectes i plans en la geometria 3D | |
|
Encara que no les hem utilitzat a la finestra d'exemple anterior, convé que investigueu sobre les comandes per al paral·lelisme.
|
|
|
Naturalment, també podem construir rectes i plans a partir dels
seus elements destacats.
Ara bé, amb les mateixes comandes tenim moltes altres possibilitats, que convé que investigueu al manual i que les experimenteu. Les fonamentals en la geometria 3D són les que mostrem en la imatge següent: |
|
|
Entre d'altres que podeu investigar, també tenim la comanda distància.
En principi a la Wiris no hi ha comandes encaminades a presentar l'equació
d'una recta o d'un pla de maneres diverses i, en concret, no està
previst escriure la recta "en forma contínua". Tanmateix,
com podeu veure en una ampliació |
|
| Tenen ortocentre els tetràedres? | |
|
En el pas de la geometria 2D a la geometria 3D es pot dir, d'alguna manera, que el rol del triangle el passa a desenvolupar el tetràedre. Però a la Wiris no tenim cap comanda per definir un tetràedre no regular... potser perquè la geometria del tetràedre no es tan coneguda com la del triangle. En la pràctica anterior vam treballar amb l'ortocentre del triangle; ara mirarem si ho podem generalitzar per al tetràedre i deixem com a possible exercici 6 l'estudi del baricentre del tetràedre. |
|
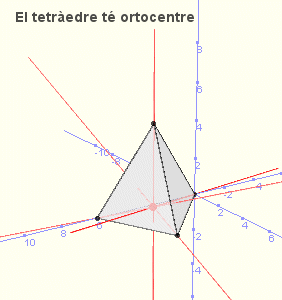
Amb l'activitat Wiris que s'obre amb la icona de l'esquerra podreu constatar que no sempre existeix ortocentre d'un tetràedre. Veureu una activitat comentada que us proposem d'estudiar.
|
|
 |
|
|
Una imatge de l'activitat de l'ortocentre del tetràedre.
Està proposada amb uns punts que configuren un tetràedre que sí que té ortocentre. Però si canvieu els punts per uns altres el més segur és que defineixin un tetràedre no ortocèntric. |
|
|
|
|