|
||||||||||||||||
| Pràctica |
|
|
|
Exercicis
|
||||||||||||
|
|
Moviments del pla |
|
|
|
|
En aquesta pràctica veurem les comandes de la Wiris per aplicar moviments a figures geomètriques. Veurem algun exemple senzill i, com a ampliació, explicarem detalladament com fer una activitat didàctica interactiva per mostrar el significat del vector de translació. En l'exercici 3 d'aquest mòdul es demana que feu una variació d'un dels exemples o, alternativament, que feu una nova activitat didàctica de l'estil de la d'aquesta pràctica (que serveix per explicar les translacions), però per explicar als alumnes la simetria axial o la simetria central. |
|
|
|
Comandes de la Wiris per treballar els moviments del pla |
| La Wiris pot calcular i dibuixar la transformació d'una figura mitjançant un moviment del pla usant les comandes rotació, simetria i translació. | |
|
|
La comanda rotació |
|
|
|
|
|
Vegeu un exemple de rotació que genera la figura de la imatge següent. Cliqueu a la icona de l'esquerra per obrir la finestra activa i practicar introduint algunes variacions. La comanda triangle_equilàter genera el triangle equilàter de centre i longitud del costat donats com a arguments. |
 |
|
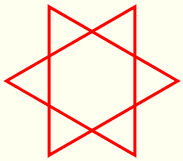
|
|
|
|
|
|
|
La comanda simetria |
| Com en altres ocasions ja s'ha comentat una mateixa comanda de la Wiris pot realitzar diverses accions segons els arguments que li passem. Això succeeis amb la comanda simetria que tant serveix per obtenir el resultat d'una simetria axial com d'una simetria central | |
| (1) La comanda simetria per a les simetries axials | |
|
|
Si volem trobar el resultat d'aplicar una simetria
axial aplicarem la comanda simetria que, en aquest
cas:
|
|
|
Si cliqueu a la icona de l'esquerra per obrir la finestra activa veureu les línies de codi que es reprodueixen tot seguit. |
 |
|
|
|
|
Ara us demanem que hi feu algunes modificacions per obtenir una figura com la següent. |
|
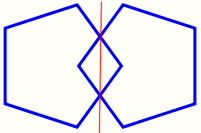 |
|
|
Figura generada aplicant una simetria a un polígon
regular de 5 costats; també es veu l'eix
|
|
|
Haureu de fer que es dibuixi l'eix i els canvis per obtenir la figura podeu provar de fer-los...
|
|
| També us proposem que construïu una diagonal del pentàgon original, cosa que podeu fer per exemple amb la comanda d = segment(T3, T5) i tot seguit podeu definir una llista que sigui el pentàgon a la diagonal: LL = {T, d}. Aleshores feu que es dibuixi la diagonal i, en comptes d'aplicar la simetria a T, apliqueu-la a LL. Observeu el resultat! | |
| (2) La comanda simetria per a les simetries axials | |
| Ja sabeu que si voleu fer una simetria
central aquesta accció és equivalent a una rotació
d'angle |
|
Però també ens serveix la comanda
simetria per a una simetria central que, en aquest
cas:
En la finestra activa que podeu obrir si cliqueu a la icona de l'esquerra en teniu un exemple.
|
|
|
|
La comanda translació |
|
|
|
|
|
Vegeu un exemple de la comanda translació que genera la figura de la imatge següent. Cliqueu a la icona de l'esquerra per obrir la finestra activa i practicar introduint algunes variacions. Observeu que la figura es genera com un conjunt de circumferències traslladades de la primera. |
 |
|
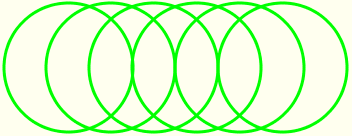
|
|
|
|
|
|
|
Una de les opcions de l'exercici 3 d'aquest mòdul consisteix a modificar l'activitat anterior per obtenir un tauler gràfic interactiu semblant al de la imatge següent, de manera que movent el punt de color negre escollim el radi de les circumferències. |
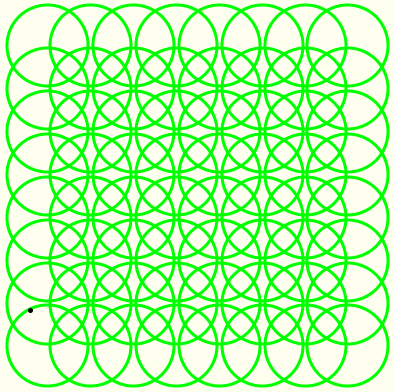
|
|
|
|
|
|
|
Activitat didàctica: translació de vector donat |
|
|
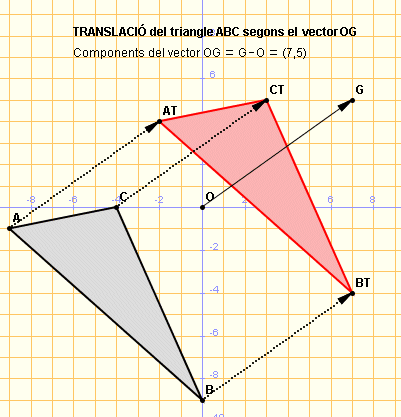
Aquesta activitat consisteix a visualitzar un triangle, un vector de translació i el triangle traslladat del primer segons aquest vector. Cliqueu a la icona de l'esquerra per veure el codi i provar el tauler gràfic interactiu.
|
|
|
|
Translació de vector OG aplicada al triangle ABC |
|
| Primer definim els elements geomètrics de partida: els vèrtexs del triangle, el triangle, els extrems del vector, el vector de translació i el vector unitari de la mateixa direcció. Aquest vector unitari el necessitarem per definir altres elements de l'activitat. | |
 |
|
| Tot seguit, apliquem la translació al triangle i als seus vèrtexs, i guardem el resultat en les corresponents variables. | |
| La Wiris no dibuixa els vectors amb la fletxa a la punta. Perquè ho faci, hem de definir i dibuixar aquesta fletxa. És aquí on ens resulta útil el vector unitari w. La fletxa és un triangle i els seus vèrtexs són l'extrem del vector i dos punts obtinguts rotant +0.2 rad i -0.2 rad, respectivament, el punt que es troba a 0.7 unitats de G en la direcció de -w. Observeu que definim la fletxa com una funció que depèn de G; d'aquesta manera, la mateixa definició servirà per a les quatre fletxes que necessitem dibuixar, ja que totes assenyalen la mateixa direcció w, però amb extrems diferents: | |
| Per dibuixar les línies de puntets que uneixen un vèrtex X amb el seu traslladat T(X) segons el vector v definim també una funció que depèn del punt d'origen X. D'aquesta manera, farem més lleugera la comanda dibuixa: | |
| Per acabar, dibuixem tots els elements amb les opcions adients i escrivim el títol de l'activitat i fem visuals les components dels vectors, amb l'objectiu que els alumnes relacionin el moviment de translació amb les components del vector: | |
 |
|