|
||||||||||||||||
| Pràctica |
|
|
|
Exercicis
|
||||||||||||
|
|
Circumferència i còniques |
|
En aquesta pràctica aprofundirem en les comandes relacionades amb la circumferència, molt en especial la comanda recta_tangent i la comanda punt_més_proper.Per això veurem dues activitats:
També es presenten algunes de les comandes més importants per definir còniques i treballar amb els seus elements. Aquesta part es pot considerar d'ampliació.
|
|
|
|
Principals comandes relacionades amb la circumferència |
|
|
|
|
La comanda circumferència,
o de manera abreujada cfr, que es pot entrar
pel teclat o amb les icones de la carpeta
Si C és una circumferència, llavors centre(C)
i radi(C) retornen el centre i el radi de la
circumferència, respectivament. |
|
|
|
Recta tangent a una circumferència en un punt de la mateixa |
|
|
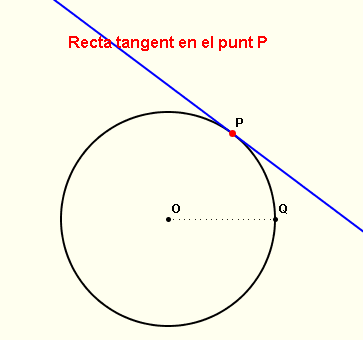
Tal com ja hem vist anteriorment, per al cas d'una recta, la comanda punt_més_proper(figura, punt mòbil)aconsegueix que quan movem un punt, la Wiris n'adapti la posició fins que estigui situat exactament sobre la figura. Aquesta figura pot ser una recta, una circumferència o, més en general, una cònica. Ara explicarem les comandes emprades en l'activitat següent que permet moure un punt P sobre una circumferència i construeix la tangent a la circumferència en aquest punt. Es pot escollir el centre i el radi de la circumferència movent els punts O i Q del tauler gràfic. És recomanable intentar reconstruir l'activitat sense obrir la finestra interactiva de l'esquerra, com a part opcional de la pràctica. |
|
|
|
Recta tangent en un punt de la circumferència |
|
|
Explicació de les comandes emprades |
|
| En primer lloc, definim el centre, un punt de la circumferència i la circumferència mateixa. A continuació, definim un punt auxiliar, que no dibuixarem, i el punt P amb la comanda punt_més _proper. D'aquesta manera, el punt P només es pot moure sobre la circumferència. Després, definim la recta tangent a la circumferència pel punt P. Podem observem que, paral·lelament a les nostres indicacions constructives, la Wiris fa geometria analítica "per sota". | |
 |
|
| Observació: la comanda recta_tangent ens estalvia la feina de definir el segment s d'extrems O i P (un radi, perquè O és el centre i P un punt de la circumferència) i després la recta perpendicualr a s en el punt P, que serà la recta tangent. Però és clar que també ho podríem fer així i el resultat seria el mateix! | |
| Si volem visualitzar el radi de la circumferència amb una línia de puntets, podem definir-la emprant una llista: | |
| Finalment, establim les propietats del tauler, dibuixem tots els elements necessaris i escrivim tots els missatges que considerem oportuns: | |
 |
|
|
|
Tangents a una circumferència per un punt exterior |
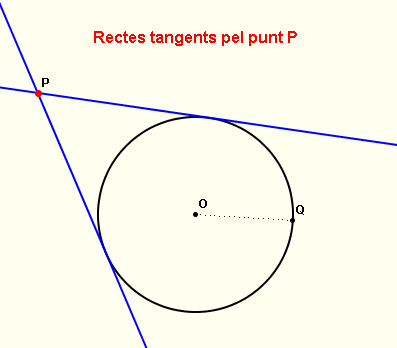
| La comanda recta_tangent només funciona si el punt P pertany a la circumferència. Si el punt P és exterior, hi ha dues rectes tangents per P que la Wiris ens dóna directament amb la comanda rectes_tangents. Cal tenir en compte que aquesta comanda només funciona si el punt P és exterior a la circumferència. | |
|
|
|
|
Rectes tangents a una circumferència per un punt exterior |
|
Segurament ja heu experimentat amb la finestra
activa que s'obre amb la icona que teniu al costat de la figura anterior
i haureu pogut veure que les dades inicials (que podrem escollir en el tauler
gràfic) seran:
i a partir d'aquí la Wiris haurà de construir les dues tangents, si pot. Les línies de codi per construir els objectes són: |
|
 |
|
| Ara bé, les rectes tangents també es poden construir trobant els punts de tangència. En aquest cas haurem d'utilitzar el fet que la tangent és perpendicular al radi en el punt de tangència i per tant el punt de tangència veu amb un angle de 90º el segment que uneix el centre O de la circumferència amb el punt P. Si fem una circumferència que tingui per diàmetre el segment OP (té centre en el punt mig d'aquest segment) els punts de tangència són els punts de tall de la circumferència inicial amb aquesta que acabem de construir perquè des d'aquests punts es veu efectivament el diàmetre indicat amb un angle de 90º. | |
| Per fer això que ha semblat tan llarg d'explicar en paraules, només haurem d'introduir unes petits modificacions en la finestra activa anterior. Recordeu que la intersecció de dues figures és una llista de punts i és per això que hem d'utilitzar els subíndexs per referir-nos als punts d'intersecció, encara que només n'hi hagi un. | |
 |
|
|
|
|
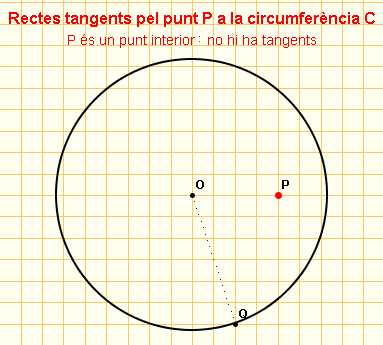
| En l'exercici 4 d'aquest mòdul, es proposa integrar les dues activitats que hem vist fins ara en aquesta pràctica en una de sola i afegir.hi quelcom, per tal de contemplar les tres possibles posicions del punt P respecte de la circumferència i que doni la resposta escaient (una recta tangent, dues o cap, amb un missatge) segons la posició del punt. | |
|
|
|
Elcas que falta comentar en l'estudi de la posició
del punt respecte de la circumferència. |
|
|
|
Comandes de la Wiris relacionades amb les còniques |
|
Per definir una cònica, la Wiris disposa de la comanda cònica
que es pot entrar amb la icona
Les comandes ellipse, paràbola i hipèrbola permeten construir còniques a partir dels seus elements característics: |
|
| La comanda ellipse rep com a arguments, per aquests ordre, el semieix major, el semieix menor, el centre i el vector director de l'eix major, o també, en lloc del vector, l'angle que forma l'eix major amb l'eix x. | |
| La comanda paràbola rep com a arguments, per aquest ordre, la distància focal, el vèrtex i el vector director de l'eix de simetria o bé l'angle que forma l'eix de simetria amb l'eix x. | |
| La comanda hipèrbola
rep com a arguments, per aquest ordre, el semieix real, el semieix imaginari,
el centre i el vector director de l'eix real o bé l'angle que forma
aquest eix amb l'eix x. |
|
|
|
|
|
Obre la finestra activa de l'esquerra on trobaràs algunes comandes relatives a còniques, a punt per practicar. Prova algunes comandades més i investiga una mica. |
|
|
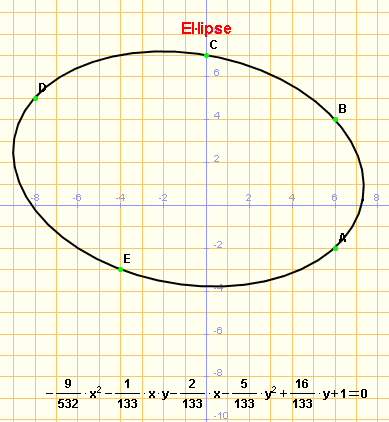
Cònica per cinc punts |
|
|
|
|
|
|
|
Per cinc punts donats del pla hi passa una única cònica. Es pot trobar l'equació d'aquesta cònica resolent un sistema de cinc equacions amb cinc incògnites (o sis incògnites, una d'elles lliure). Posteriorment, classifiquem la cònica trobada emprant els coeficients de la seva equació. La Wiris ens resol aquest problema d'una forma ben senzilla, construint un tauler gràfic interactiu on podrem moure els cinc punts. Observeu que en aquesta activitat es manté la malla visible per poder aconseguir fàcilment tres punts alineats i, per tant, una cònica "degenerada" que consisteix en un parell de rectes. Cliqueu a la icona de l'esquerra per "jugar" amb el tauler gràfic i veure com la Wiris classifica la cònica i n'escriu l'equació. |
| Aquesta activitat és ben senzilla de programar: definim els punts i la cònica, els dibuixem i escrivim el domini i l'equació. | |
 |
|
|
|
Construcció de la paràbola a partir de la directriu i el focus. Lloc geomètric |
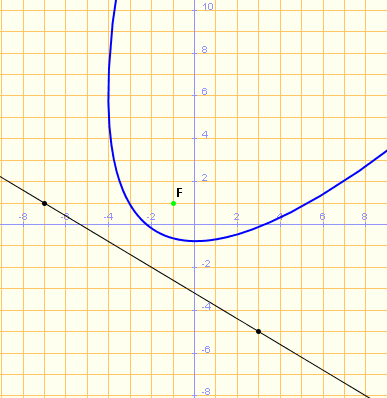
| En aquest apartat dissenyem una activitat per mostrar que la paràbola és el lloc geomètric dels punts que equidisten de la directriu d i el focus F. Primer de tot, definim bé quin és l'objectiu: volem un tauler de la Wiris amb una paràbola que s'actualitzi en moure la directriu i el focus (s'hauran de dibuixar els dos punts utilitzats per definir la directriu, a més del focus F). A continuació, tal com es proposa en una de les opcions de l'exercici 4 d'aquest mòdul, caldrà definir i dibuixar un punt mòbil M sobre la directriu (emprant punt_més_proper), traçar la mediatriu de M i el focus F i tallar-la amb la paral·lela a l'eix que passa per M. Aquest punt de tall P estarà sobre la paràbola i mostrarà que P equidista del focus i de la directriu. | |
|
|
|
Paràbola interactiva amb la directriu i el focus |
|
|
|
Les dades inicials són la directriu (definida
a partir de dos punts, A i B) i el focus F. Però
la comanda paràbola vol com a arguments
la distància focal, el vèrtex i el vector director de l'eix,
que els hem de calcular prèviament. Observeu que si oblideu fer alguna
assignació amb |
 |
|
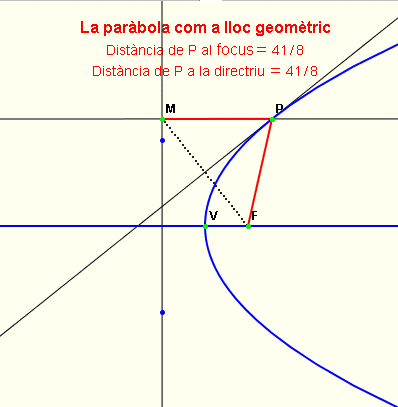
| Si heu triat d'estudiar aquesta part de la pràctica, que ja hem dit que es podia considerar d'ampliació, i us apeteix presentar-lo ja podeu anar cap a la segona opció de l'exercici 4 d'aquest mòdul: completar l'activitat anterior per mostrar que els punts P de la paràbola equidisten del focus i de la directriu. L'objectiu és obtenir un tauler gràfic interactiu semblant al de la imatge següent: | |
|
|
|
Els punts de la paràbola equidisten del focus i de la directriu |
|