Enrera
 Mòdul 2
Utilització de l' Aula de Noves Tecnologies per a la Ciència
  Pràctica
1
2
3
4
            
Exercicis
Exercicis
 
 

Objectius
   
 

L'objectiu d'aquesta pràctica és:

  • Aprendre a utilitzar les principals eines d' anàlisi de dades.
   
L' EQUIP MULTILOG I EL PROGRAMA MULTILAB
Pràctica E. Anàlisi de dades
   
  Ja heu vist que els cursors informen de les coordenades X i Y d'un punt i de les diferències entre dos valors de coordenades, dX i dY, a més d'1/dt. Per altra banda, podeu obtenir més informació, com l'equació del gràfic, amb les eines d' anàlisi del menú corresponent.
   
Les eines d' anàlisi només poden aplicar-se al conjunt de dades que es mostren a la finestra del gràfic. Si teniu un únic cursor sobre el gràfic, l' anàlisi actua sobre totes les dades. Si useu dos cursors, l' anàlisi es farà sobre la zona seleccionada.
   
  Ajustament de la corba
   
 

 

  • Obriu de nou el projecte "Dog's Cave".
  • Amb Commuta primer cursor i Commuta segon cursor , inseriu dos cursors damunt del gràfic Graph 1.
  • Arrossegueu-los i seleccioneu del gràfic oxigen-temps un marge de dades que vagi des que s' aboca el CO2 fins que torna a augmentar la concentració d' oxigen.
  • Pregunta:

    Quina és l'equació de descens de concentració d' oxigen?

Per respondre, ajustareu les dades a una corba que determini aquesta equació.

 
 
  • Feu clic a Ajudant d' anàlisi , a la barra d' eines principal.
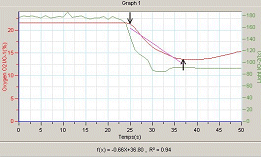
  • Seleccioneu:
    • Basat en conjunt de dades Exp 13-Oxygen O2 I/O1
    • Tipus lineal
    • Mostra equació gràfic
    • Mostra R2 gràfic
   
  • Noteu que apareix la recta de regressió determinada mitjançant el mètode dels mínims quadrats.


    A la barra d' informació del gràfic es mostra l'equació i el valor del coeficient de correlació R2 que determina la bondat de l' ajustament.
 
 
 
Una corba s'ajusta correctament al conjunt de dades quan el coeficient de correlació R2 és molt pròxim a ± 1.
   
 
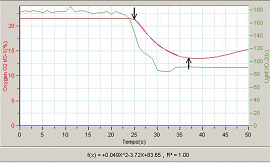
  • Com que sembla que les dades seleccionades s'ajusta a una paràbola, ajustareu les dades a una corba de tipus polinomial d'ordre 2 (paràbola) i li demanareu que us determini el coeficient de correlació.
   
 

  • Noteu que aquesta corba s'ajusta millor a les dades, ja que R2 = 1,00, i que els dos ajustaments que heu fet apareixen al mapa de dades com a:

    Lineal (Oxygen O2 I/O-1) i Polinomial (Oxygen O2 I/O-1)
 
  • Elimineu l' ajustament lineal del mapa de dades i editeu un gràfic que contingui només les dades de l' ajustament polinomial davant del temps.
  • Anoteu l'equació i el coeficient de correlació de l' ajustament parabòlic.
  • Doneu un nom a la gràfica i afegiu-la al projecte .
  • Guardeu el projecte amb el nom m2_e2 a la carpeta m2.
  Com podeu comprovar amb la pestanya Ajust de corba, l' ajudant d' anàlisi pot ajustar dades a les corbes següents:
 
   
 

Promitjant
 

 

A la finestra d' ajudant d' anàlisi hi ha una eina amb el nom Promitjant que permet suavitzar un gràfic. És una eina útil per reduir sorolls fortuïts, especialment si es vol aplicar qualsevol funció d' anàlisi a les dades. El procés de suavització consisteix a substituir cada punt del gràfic amb la mitjana dels seus punts veïns. Recordeu que la suavització d'un gràfic també es pot fer amb el botó de la barra de gràfic Més suau.
 

 

  • Suavitzeu les dades de llum corresponents a l'Experiència 13 a partir de l' ajudant d' anàlisi. Noteu que les dades resultants poden substituir les originals o bé aparèixer en una nova finestra.
  • Determineu l'equació de descens de llum a partir de la gràfica suavitzada pel mateix rang de dades anterior i compareu les dues equacions.
  • Editeu el gràfic, doneu-li un nom i afegiu-lo al projecte .
  • Guardeu el projecte amb el nom m2_e2 a la carpeta m2. Aquest projecte llevareu més endavant al tutor/a com a exercici d'aquesta pràctica.
   
  Funcions
   
 

Així mateix, l' ajudant d' anàlisi disposa d'un seguit de funcions que permeten fer càlculs a partir de les dades experimentals.

 

Especialment útil pot resultar la funció Delta Y:
 

 

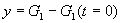Aquesta funció dibuixa una línia de la diferència entre la coordenada Y de cada punt i la coordenada Y del primer punt. Fareu servir aquesta funció per fer coincidir el primer punt amb l'origen de coordenades.

  • Exploreu la finestra Funcions de l' ajudant d' anàlisi.
   
  Ajustament manual de corba
   
 

Aquesta eina del menú Anàlisi de la barra principal permet dibuixar una corba matemàtica, canviar els paràmetres de la corba fins que encaixin dins del conjunt de dades, i mostrar l'equació resultant.


Hi ha quatre tipus de corbes matemàtiques que es poden dibuixar: lineal, quadràtica, exponencial i potencial.

   
 

  • Obriu de nou el projecte "Dog's Cave".

  • Tanqueu totes les finestres menys la de gràfic i el mapa de dades.

  • Des del Mapa de dades oculteu les dades del sensor de llum.
  • Amb Commuta primer cursor i Commuta segon cursor inseriu dos cursors damunt del gràfic Graph1.
  • Arrossegueu-los i seleccioneu del gràfic oxigen-temps el mateix marge de dades que heu seleccionat anteriorment i que va des que s' aboca el CO2 fins que torna a augmentar la concentració d' oxigen.
  • Seleccioneu Gràfic | Retalla, retalleu la gràfica i afegiu gràfic al projecte . Ara us apareix al mapa de dades el Gràfic 2.
  • Obriu el menú Anàlisi | Ajustament manual de corba i us apareixerà la pantalla següent:
 
   
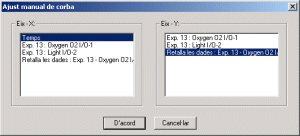  • Seleccioneu Temps a l'eix X i Retalla les dades: Exp 13: OxygenO2 I/O-1 a l'eix Y.
  • Premeu D' acord.
  • Noteu que us apareix una finestra amb la gràfica Exp 13: OxygenO2 I/O-1 versus Temps i una recta amb la seva equació.
   
 
 
  • A les pestanyes de color blau corresponents a la forma de la corba, seleccioneu la corba quadràtica.
  • Noteu com ara us canvia la pantalla anterior, que té dues files de cursos, per la següent, que en té tres.
   
   

Sota la gràfica apareix l'equació d'una paràbola de fórmula f(x) = A(x + B)2 + C

Movent els cursors de les files A, B i C, canviareu els valors d'aquests paràmetres i us apareixerà una corba de color negre que podreu ajustar damunt de l' anterior de color vermell.
 
  • Moveu els cursors fins que aparegui la corba corresponent a l' ajustament manual.
   
   
  • Desplaceu el cursor C fins que els extrems de cada corba coincideixin.
  • Continueu fent desplaçar els cursors fins a fer coincidir aquesta corba amb l' anterior i que l'equació d'aquesta corba coincideixi amb la que heu trobat amb l' ajudant d' anàlisi.
  • Finalment, tindreu la corba ajustada manualment, i a la finestreta de sota us apareixerà las seva equació expressada en la forma f(x) = A(x + B)2 + C.
 
  Estadística
   
 

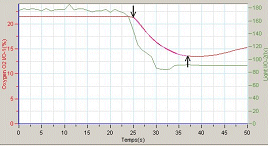Marqueu les posicions indicades en la figura i activeu l' opció del menú Anàlisi | Estadística, d'aquesta manera totes les dades estadístiques es referiran a l' interval entre els cursors. En el cas que únicament es marqui la corba amb el primer cursor, les dades estadístiques es refereixen a tota la corba.

Apareixerà la següent finestra:
 



  Observeu dades estadístiques com la mitjana, desviació estàndard, màxim, mínim, suma, àrea, nombre de mostres i freqüència de mostreig.
   
   
   
   
 
Amunt