| |
Objectius |
| |
- Dissenyar una activitat de tractament de vídeo digital amb
el programa Multilab, utilitzant el marcatge consecutiu d'un únic
objecte en cada fotograma.
- Fer un estudi complet del moviment d'una pilota de bàsquet,
en un llançament lliure a cistella, des que comença
fins que arriba a prop de terra. Això suposa:
- Identificar en el gràfic les diferents etapes del moviment.
- Determinar les equacions del moviment de la pilota a l'eix x
i a l'eix y en funció del temps a les diferents etapes.
- Trobar l'equació de la trajectòria y(x) des
que la pilota deixa d'estar en contacte amb la mà de la
noia fins que toca la cistella.
|
| |
|
| |
Estudi del moviment del llançament a
cistella d'una pilota de bàsquet |
|
|
|
 |
Introducció |
| |
|
|
|
En la següent experiència es tracta de dissenyar una activitat
de tractament de vídeo en la qual s'estudia un llançament
a cistella.
Aquest llançament, com veureu en el vídeo, consta de tres
parts:
- Una primera part que consisteix a impulsar la pilota, mentre aquesta
està en mans de la noia.
- La segona correspon a un tir parabòlic i és el moviment
de la pilota des que deixa d'estar en contacte amb la mà de
la noia, fins que toca la cistella.
- La tercera i última part correspon al moviment de caiguda lliure
de la pilota des de la cistella al terra.
|
| |
|
|
|
Passos a seguir |
|
|
|
| |
- Observar el moviment en el vídeo.
- Assenyalar les diferents parts, explicar els diferents tipus de moviments
i dibuixar les gràfiques de la predicció del moviment.
- Configurar el sistema de mesura.
- Enregistrar dades: això vol dir marcar les posicions de la
pilota en el vídeo.
- Comparar les gràfiques obtingudes amb les prediccions.
- Transformar les gràfiques i fer els retalls dels trossos que
interessi analitzar.
- Analitzar les gràfiques i fer càlculs: equacions del
moviment, velocitat, acceleració, etc.
- Descriure completament el moviment de la pilota.
- Aplicar els resultats a altres situacions.
|
| |
|
 |
Predicció |
| |
|
| |
Per caracteritzar el moviment i fer la predicció de les diferents
gràfiques, cal observar el vídeo prèviament.
Obriu el programa Multilab  . Com que no tindreu la consola connectada, us sortirà el missatge
que indica que no pot connectar amb l'enregistrador. Digueu D'acord; feu clic a sobre la icona . Com que no tindreu la consola connectada, us sortirà el missatge
que indica que no pot connectar amb l'enregistrador. Digueu D'acord; feu clic a sobre la icona  ,
que activa l'opció de tractament de vídeo digital. Per
obrir el vídeo, feu clic a sobre de la icona ,
que activa l'opció de tractament de vídeo digital. Per
obrir el vídeo, feu clic a sobre de la icona  ,
seleccioneu el vídeo ,
seleccioneu el vídeo  , que ja havíeu descarregat prèviament i que es troba en
el directori m4a i feu clic en Obrir.
, que ja havíeu descarregat prèviament i que es troba en
el directori m4a i feu clic en Obrir.
S'obrirà el vídeo a la finestra gran; utilitzeu els botons
convencionals de reproducció de vídeo per tal d'observar
el moviment de la pilota  . . |
| |
|
| |
- Quines són les diferents parts del moviment de la pilota?
- Com definiries aquestes parts? MRU, MRUA, tir parabòlic,
moviment amb acceleració constant, moviment accelerat, etc.
- Intenteu dibuixar de manera aproximada la forma que al vostre parer
tindran els gràfics x-t i y-t corresponent al moviment de la
pilota, des del moment en què la jugadora la comença a moure
(primer fotograma) fins que aquesta arriba a prop del terra després
de passar per la cistella.
|
| |
|
| |
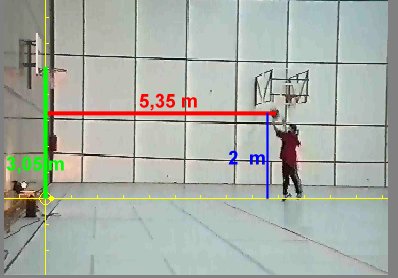
En la figura de dalt es troben algunes dades que us poden resultar útils
per fer la predicció: la pilota és llança a una distància
de 5,35 m de la cistella, a una alçada de 2 m, la cistella es troba
a 3,05 m del terra. La duració del tir parabòlic és
aproximadament d'1 s i la caiguda de la pilota de la cistella al terra
dura aproximadament 0,7 s. El sistema de referència es troba marcat
en groc a la figura.
Feu també la predicció de les gràfiques Vx-t i Vy-t.
Suposeu que les components Vx i Vy de la velocitat, a l'instant en què
la pilota surt de les mans de la jugadora, tenen un valor en mòdul
aproximadament de 4 m/s i de 8 m/s, respectivament. |
| |
|
 |
Al final de la pràctica hi ha una icona per descarregar
la pràctica en format Word, a fi que l'alumnat pugui utilitzar-la directament
com a protocol. Podeu imprimir la pràctica i utilitzar
les quadrícules que hi ha per fer la predicció dels gràfics. |
| |
|
| |
.. |
| |
|
| |
Configuració del sistema de mesura |
| |
|
| |
- Deixeu el vídeo al primer fotograma clicant el botó
Començar
 . .
- Seleccioneu els colors per marcar la posició de la pilota,
dels eixos i de l’escala. Utilitzeu el botó Mostrar
color
 de la barra d’eines de sota la finestra del vídeo. Escolliu
els colors a cada casella (és convenient que els colors triats
destaquin del fons).
de la barra d’eines de sota la finestra del vídeo. Escolliu
els colors a cada casella (és convenient que els colors triats
destaquin del fons).
- Per calibrar el videoclip, cliqueu la icona Escala
 . S'obre una finestra on heu d'escriure a la casella dimensió
actual (cm) el valor de la longitud indicada, en cm, que us
apareix en el primer fotograma del vídeo. Abans de prémer D'acord, marqueu dos punts, fent clic amb el ratolí,
a cada un dels extrems de la longitud assenyalada com a 305 cm. Veureu
que els dos punts us quedaran units per una ratlla discontínua
formant un segment; si el segment no us ha quedat ben igual a la longitud,
podeu ajustar-lo movent l’extrem amb el ratolí fins a fer-lo
coincidir. Per finalitzar la calibració premeu D'acord. . S'obre una finestra on heu d'escriure a la casella dimensió
actual (cm) el valor de la longitud indicada, en cm, que us
apareix en el primer fotograma del vídeo. Abans de prémer D'acord, marqueu dos punts, fent clic amb el ratolí,
a cada un dels extrems de la longitud assenyalada com a 305 cm. Veureu
que els dos punts us quedaran units per una ratlla discontínua
formant un segment; si el segment no us ha quedat ben igual a la longitud,
podeu ajustar-lo movent l’extrem amb el ratolí fins a fer-lo
coincidir. Per finalitzar la calibració premeu D'acord.
- Per situar l'origen de coordenades, feu clic a la icona Situar
l'origen
 ,
assenyaleu amb el ratolí el punt on vulgueu establir l'origen;
l'origen el podeu establir al centre de la pilota en el primer fotograma,
o a l'extrem de sota de la longitud indicada de 3,05 m en el primer
fotograma. Premeu D’acord. ,
assenyaleu amb el ratolí el punt on vulgueu establir l'origen;
l'origen el podeu establir al centre de la pilota en el primer fotograma,
o a l'extrem de sota de la longitud indicada de 3,05 m en el primer
fotograma. Premeu D’acord.
|
| |
|
 |
Enregistrament de dades |
| |
|
| |
- Feu clic amb el ratolí en el centre de la pilota per marcar
la seva posició. Veureu que a la taula apareixen els valors x,
y, t d'aquest punt i el vídeo passa al fotograma següent.
Torneu a marcar amb el ratolí la nova posició de la pilota
i així successivament fins a l'últim fotograma en què
la pilota ja està a prop del terra. Tingueu cura de marcar sempre
en el centre de la pilota; les desviacions són les que introdueixen
els errors en la mesura.
- Una vegada obtinguts els gràfics x-t i y-t del moviment de
la pilota, situeu el cursor en qualsevol punt d’un d’ells,
i moveu-lo amb el ratolí mentre observeu en el vídeo les
posicions de la pilota que acabeu de marcar. Feu el mateix amb l’altre
gràfic. Fixeu-vos si estan ben situats els punts que assenyalen a cada fotograma
la posició de la pilota.
|
 |
Si hi ha algun punt que heu marcat erròniament,
podeu corregir-lo de la manera següent. Situeu-vos al fotograma corresponent, utilitzant
els botons Fotograma anterior o següent. A continuació moveu
el punt marcat, amb el ratolí, fins a col·locar-lo en la posició
adequada. Veureu que tant el gràfic de posició (X,Y-t) com
la taula queden actualitzats.
|
 |
|
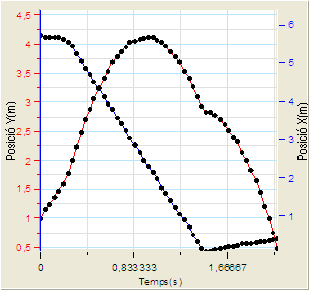
|
A la imatge de l'esquerra es pot observar el
gràfic que ha de sortir després del marcatge de tots
els punts del moviment de la pilota. |
|
| |
|
| |
Guardeu l’arxiu, amb el botó Guardar  de la barra d’eines principal, al directori m4a.
Doneu-li el nom m4a_p3; observareu que s'ha gravat amb
l'extensió vap. Si teniu el vídeo associat basquet.avi en
aquest mateix directori, després, quan obriu el projecte a través
de l'opció del menú Arxiu | Obrir projecte d'anàlisi
de vídeo, s'obrirà el projecte amb el vídeo
i totes les gràfiques que teníeu fins al moment de gravar.
de la barra d’eines principal, al directori m4a.
Doneu-li el nom m4a_p3; observareu que s'ha gravat amb
l'extensió vap. Si teniu el vídeo associat basquet.avi en
aquest mateix directori, després, quan obriu el projecte a través
de l'opció del menú Arxiu | Obrir projecte d'anàlisi
de vídeo, s'obrirà el projecte amb el vídeo
i totes les gràfiques que teníeu fins al moment de gravar. |
| |
|
| |
Comparació amb les prediccions de
les gràfiques posició-temps |
| |
|
| |
Compareu els gràfics de posició
de la vostra predicció amb els gràfics obtinguts. En què
són similars i en què difereixen? |
| |
|
 |
Per treballar millor els gràfics, és
convenient que aquests apareguin més grans i al centre de la pantalla.
Per poder fer el canvi de lloc de les finestres, cliqueu el botó
Taula  . Veureu que aquesta desapareix; si voleu que torni a aparèixer, torneu
a clicar Taula. . Veureu que aquesta desapareix; si voleu que torni a aparèixer, torneu
a clicar Taula.
Per tal d'explorar les diferents parts de la gràfica
i relacionar-les amb el vídeo, podeu situar el cursor en qualsevol
part de la gràfica, fent clic a la icona  ;
amb les tecles de cursor del teclat podeu moure la fletxa i a la vegada
es mourà la pilota en el vídeo. A la part baixa del gràfic
apareixen les coordenades x o y i el temps corresponents a cada punt de
la gràfica. ;
amb les tecles de cursor del teclat podeu moure la fletxa i a la vegada
es mourà la pilota en el vídeo. A la part baixa del gràfic
apareixen les coordenades x o y i el temps corresponents a cada punt de
la gràfica. |
| |
|
| |
Expliqueu les diferents parts de la gràfica en relació
al moviment de la pilota, per exemple:
- De 0 a 0,28 s, la pilota roman a la mà de la noia i va adquirint
velocitat: és un moviment accelerat a l'eix x i a l'eix y.
- De 0,28 a 1,4 s, la pilota fa un tir parabòlic, és a
dir, una combinació de un MRU en la direcció de l'eix X
(gràfica corresponent a una línia recta) i un MRUA en
la direcció de l'eix Y (gràfica corresponent a una paràbola).
- D'1,56 a 2,12 s, la pilota fa una caiguda lliure. Queda un interval
de temps (d'1,4 a 1,56s) que correspon al moment en què la pilota és a la cistella, difícil de descriure i del qual podeu prescindir.
Comproveu que aquests intervals de temps coincideixen amb la vostra gràfica.
|
| |
|
 |
Transformació de les dades |
| |
|
| |
Un cop feta l'anàlisi qualitativa de les diferents
parts de la gràfica, podeu passar a transformar les dades; això
vol dir retallar els trossos de gràfica corresponents al tir parabòlic,
relacionar les variables x i y en una mateixa gràfica i obtenir els
gràfics Vx,Vy-t. |
| |
|
| |
Gràfics de posició |
| |
|
| |
Tir parabòlic
- Retalleu els gràfics corresponents al tir parabòlic.
Situeu els dos cursors a les posicions 0,28 s
 i 1,54 s
i 1,54 s  .
Activeu l'opció del menú Gràfic | Retalla,
es retallaran els dos gràfics x(t) i y (t) i quedarà
un gràfic com el de la figura. .
Activeu l'opció del menú Gràfic | Retalla,
es retallaran els dos gràfics x(t) i y (t) i quedarà
un gràfic com el de la figura.
|
 |
|
| |
|
| |
Gràfic y-x de tot el movimentx |
| |
Ara treballareu el gràfic
y-x. Per tenir-lo en pantalla heu d'activar l'opció del menú
Gràfic | Editar gràfic, de manera que se seleccionen
les opcions tal i com es troben a la imatge següent, poseu-li y-x,
com a títol del gràfic. Afegiu el gràfic al projecte.
 .
. |
| |
|
| |
|
| |
|
 |
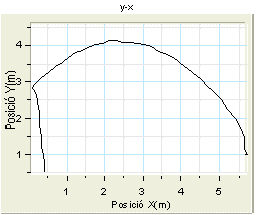 |
El gràfic y-x ha de tenir l'aspecte del de la figura
de l'esquerra. |
|
| |
|
| |
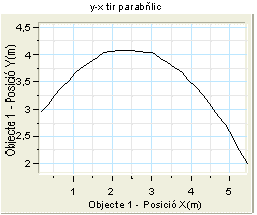
Gràfic y-x del tir parabòlic
|
| |
El següent pas serà obtenir el gràfic y-x únicament
del tir parabòlic, per després obtenir l'equació
de la trajectòria. Per tenir en pantalla el gràfic y-x del
tir, caldrà seguir els mateixos passos que en el de tot el moviment,
però seleccionant les opcions:
Eix-X: Retalla les dades: Objecte 1-Posició X
Eix-y: Retalla les dades: Objecte 1-Posició y
Poseu-li de títol y-x tir parabòlic i afegiu el
gràfic al projecte  |
 |
| Ha de sortir un gràfic com el de la figura
de la dreta. |
 |
|
| |
|
| |
Gràfics de velocitat |
| |
|
 |
Per obtenir els gràfics de velocitat,
haureu de tornar a posar en pantalla els gràfics originals de posició
i fer la derivada. Recordeu que se situa una fletxa de cursor  i es fa la derivada
i es fa la derivada  consecutivament en cadascun dels dos gràfics de posició.
Amagueu posteriorment els gràfics de posició i deixeu únicament
els de velocitat; situeu cadascun dels dos gràfics en una pantalla
diferent, de manera que al final han de quedar uns gràfics similars
a aquests:
consecutivament en cadascun dels dos gràfics de posició.
Amagueu posteriorment els gràfics de posició i deixeu únicament
els de velocitat; situeu cadascun dels dos gràfics en una pantalla
diferent, de manera que al final han de quedar uns gràfics similars
a aquests:
|
 |
|
| |
|
| |
Guardeu l’arxiu amb el botó Guardar  de la barra d'eines principal.
de la barra d'eines principal. |
| |
|
 |
Anàlisi de les dades i càlculs amb
les gràfiques posició-temps |
| |
|
| |
A les gràfiques transformades els ajustareu
les funcions matemàtiques que millor encaixin. Tenim en compte la
forma de la gràfica i els coneixements cinemàtics sobre gràfiques
corresponents al MRU i MRUA. |
| |
|
| |
Gràfiques de posició |
| |
|
| |
Gràfica x-t del tir parabòlic:
|
| |
Poseu únicament en pantalla les gràfiques
del retall x,y-t corresponents al tir parabòlic.
Situeu el primer cursor  al gràfic x-t i ajusteu-li una recta. Feu clic a la icona de
l'Ajudant d'anàlisi
al gràfic x-t i ajusteu-li una recta. Feu clic a la icona de
l'Ajudant d'anàlisi  ;
s'obrirà una finestra en la qual heu de seleccionar les següents
opcions: ;
s'obrirà una finestra en la qual heu de seleccionar les següents
opcions: |
| |
|
| |
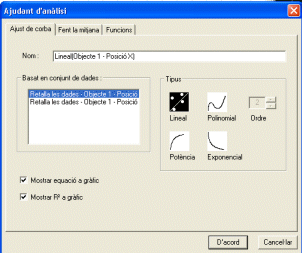 |
- A la finestra Basat en conjunt de dades
us ha d'aparèixer Retalla les dades-Objecte 1-Posició
X seleccionat.
- .Seleccioneu:
- Tipus: lineal
- Mostrar equació gràfic
- Mostrar R2 gràfic
- Premeu D'acord.
- S'ajustarà una línia recta i sortirà la
seva equació: x= -4,52t +5,40, com podeu observar a la
figura.
|
|
 |
|
| |
|
| |
Gràfica y-t del tir parabòlic |
| |
|
| |
Feu el mateix amb el gràfic y-t, ara la gràfica que heu
d'ajustar és una polinomial d'ordre 2 que correspon a una paràbola.
La funció que us ha de sortir ajustada a aquest conjunt de punts
és:
y= - 4,82 t2 + 6,39 t + 1,99 |
| |
|
| |
Gràfic y-x del tir parabòlic
|
| |
|
| |
Torneu a posar en pantalla únicament el gràfic y-x, tal
i com heu fet anteriorment.
- Ajusteu-li al gràfic y-x del tir parabòlic la funció
que creieu convenient, mitjançant l'opció del menú
Anàlisi | Ajust manual de corba.
|
 |
Quan tenim en pantalla un gràfic de dues
variables obtingudes prèviament com a funció del temps, aquest
no es pot ajustar automàticament; per tant el gràfic y-x del tir
parabòlic s'haurà d'ajustar manualment, tal i com s'ensenya
en el mòdul 2, pràctica 2:
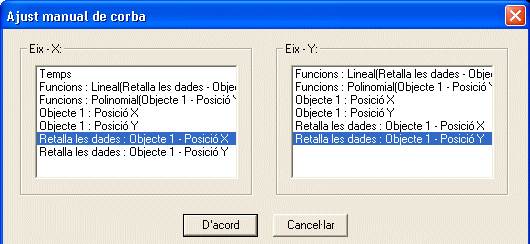
Ajustament manual de corba. Activeu l'opció del menú
Anàlisi | Ajust manual de corba; a la finestra que surt
seleccioneu les opcions que apareixen en blau a la imatge de sota i feu
clic a D'acord.
|
| |
|
| |
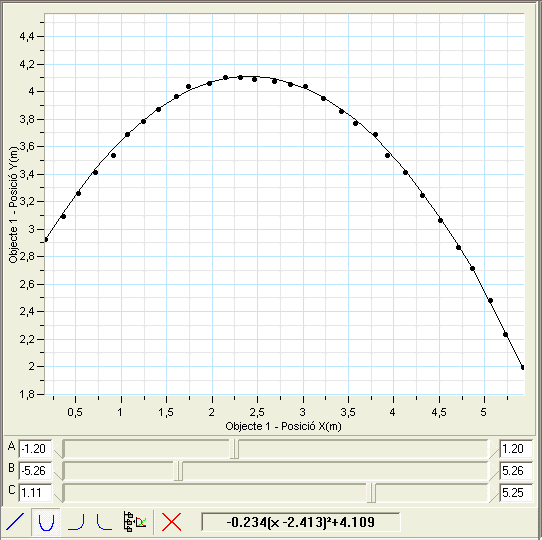
Després d'ajustar manualment la corba,
el resultat és molt similar al de la figura de sota. En línia
contínua es pot veure la gràfica ajustada, els punts indiquen
els corresponents punts experimentals. |
 |
|
| |
L'equació d'aquesta paràbola és:
y = -0,234 (x - 2,413)2 + 4,109 , que si s'eliminen parèntesis
queda: y = - 0,234 x2 +1,129x+2,746 . Si voleu, podeu calcular
els valors de x i de y per y màxima fent la derivada i igualant a zero. El resultat
és xmàx = 2,41 m i ymàx = 4,10 m , que coincideixen
força bé amb els valors en la gràfica xmàx
= 2,312 m i ymàx = 4,104 m.
|
| |
Guardeu l’arxiu amb el botó
Guardar  de la barra d'eines principal.
de la barra d'eines principal. |
| |
|
| |
Comparació amb les prediccions
de les gràfiques velocitat-temps |
| |
|
| |
Poseu en pantalla únicament els gràfics Vx-t
i Vy-t
1. Compareu els gràfics de velocitat de la vostra
predicció amb els gràfics obtinguts. En què són
similars i en què difereixen?
2. Relacioneu els trossos de les gràfiques Vx-t i Vy-t amb el moviment
de la pilota i amb les gràfiques de posició, tal i com s'ha
fet en el cas de les gràfiques de posició, per exemple:
- De 0 a 0,28 s, la pilota roman a la mà de la noia i va adquirint
velocitat: és un moviment accelerat a l'eix x i a l'eix y.
- De 0,28 a 1,4 s, la pilota fa un tir parabòlic, és a
dir, una combinació de un MRU en la direcció de l'eix X,
en el qual es pot observar que Vx és pràcticament constant,
i un MRUA en la direcció de l'eix Y, ja que a la gràfica
Vy-t se li pot ajustar una recta.
- D'1,52 a 2,12 s, la pilota fa una caiguda lliure. Es pot observar
que Vx és pràcticament zero. Al tros de gràfic
Vy-t se li pot ajustar una línia recta, tal i com correspon a
una caiguda lliure.
Queda un interval de temps (d'1,4 a 1,56s), que correspon al moment en què
la pilota és a la cistella, difícil de descriure i
del qual podeu prescindir.
|
| |
|
 |
Anàlisi de
les dades i càlculs amb les gràfiques velocitat - temps |
| |
|
| |
Ajustareu als trossos
de gràfica Vx,Vy-t, als quals correspongui un MRU o MRUA, les funcions adients,
per poder obtenir valors de velocitat i acceleració. |
| |
Situeu a les pantalles
1 i 2 els gràfics Vx-t i Vy-t respectivament. |
| |
Col·loqueu els cursors en els temps 0,28 i 1,4 s a cadascuna
de les dues gràfiques consecutivament i ajusteu una línia
recta a cada gràfica. Els resultats són:
Vx= 0,021 t - 4,52
Vy = -9,52 t + 8,96
Col·loqueu els cursors en els temps 1,52 i 2,12 s de la gràfica
Vy-t (Pantalla 2) i ajusteu-li una línia recta. El resultat serà
l'equació següent: Vy = - 9,30 t + 13,064
|
| |
Guardeu l'arxiu amb
el botó Guardar  de la barra d'eines principal.
de la barra d'eines principal. |
| |
|
| |
|
 |
Conclusions experimentals |
| |
|
| |
- Quines són les equacions,
de posició i de velocitat, del moviment corresponent al tir parabòlic? Escriviu les equacions de les components
x(t), y(t), Vx(t) i Vy(t) i les equacions vectorials de r i v.
- Compareu els resultats dels càlculs de les diferents magnituds del moviment
obtinguts a partir de les equacions de posició amb els obtinguts a partir de
les equacions de velocitat.
- Quin és el significat de cadascun dels valors numèrics
que apareixen en les diferents equacions?
- Què representa el gràfic y-x i quin és el significat
físic de l'equació y(x)?
- Descriviu de nou el moviment de la pilota. Heu de detallar cadascuna
de les parts del moviment amb els seus valors numèrics de posició
inicial, velocitat inicial, acceleració, etc.
|
 |
Per ajudar els alumnes a identificar la gràfica y-x amb la
trajectòria de la pilota i a diferenciar-la de la
y-t, pot ser una bona idea que situïn la fletxa de cursor del Multilab
en la posició més extrema de y i amb la tecla de cursor
d'avançament del teclat vagin movent la posició de la fletxa
en el gràfic. Observaran com la fletxa retrocedeix seguint la trajectòria
de la pilota. També pot ajudar la reproducció del vídeo
 ,
a la vegada que s'observa el gràfic y-x. ,
a la vegada que s'observa el gràfic y-x.
|
| |
|
| |
| Descàrrega de la pràctica
en format Word |
 |
|
| |
|
|
|
|
|
 |