| |
Ja es va comentar en el mòdul 1 que la Wiris té
dos modes de treball (o estats) per a la realització de
gràfics i per l'aplicació de comandes de geometria, 2D
(l'estat per defecte) i 3D.
-
A la carpeta d'icones 
hi ha dos botons que permeten establir el mode de treball com 2D o
3D. Recordeu-ho:

Aquests botons són equivalents a les comandes estat_geometria("3D")
i estat_geometria("2D").
- Si hem establert com a 3D l'estat o mode de treball
de la Wiris, aleshores no caldrà escriure les comades que s'indiquen
com dibuixa3d, o bé escriu3d (que ja podeu imaginar
que és la comanda per escriure text en un tauler 3D) o bé
tauler3d sinó que, en aquest cas, les comandes dibuixa,
escriu, tauler, s'interpreten ja per a gràfics tridimensionals.
També en l'exemple que encapçala aquesta pràctica
es veu que, per a la representació de gràfics tridimensionals,
en el tauler gràfic de la Wiris ha aparegut un cub de representació,
on es mostra una representació en perspectiva de la figura que
hem demanat.
En el mateix tauler gràfic disposem d'eines per a
canviar el punt de vista i la mida de la figura.
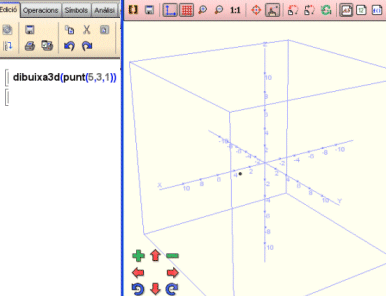
Així, per exemple, si fem dibuixar un
punt obtenim:
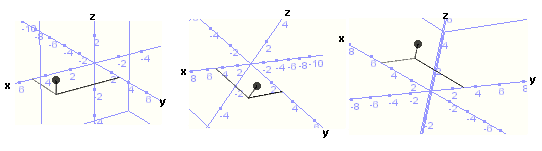
Vegeu també el dibuix del punt anterior
(on s'hi han afegit tres segments que situen el punt en relació
amb als eixos de coordenades) des de tres punts de vista
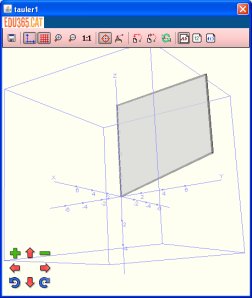
O bé comproveu com "l'estrany polígon"
que apareixia en laimatge inicial de la pràctica, des d'un altre
punt de vista apareix efectivament un polígon (com el que és!):
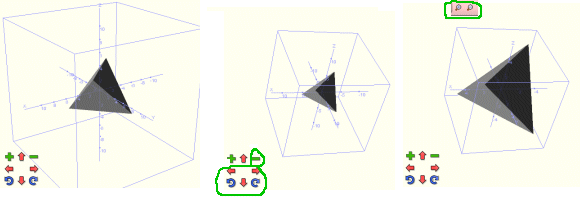
Tot seguit vegeu tres representacions d'un
mateix tetràedre. A partir de la comanda
dibuixa3d(tetraedre(10))
s'ha obtingut el gràfic d'un tetraedre regular d'aresta 10 centrat
en l'origen de coordenades.
- Amb els botons que tenim a dintre del tauler gràfic
n'hem canviat l'orientació i la mida del cub de representació.
- Amb els botons de zoom de la barra d'eines del tauler
gràfic hem canviat la mida de la figura visualitzada, és
a dir, equivalentment els intervals de x, y, z representats. En el gràfic
inicial i en el segon la zona representada és, aproximadament
x, y, z en -11..11,-11..11,-11..11 i, en canvi, en el tercer
gràfic és, també aproximadament, x, y, z en
-5..5,-5..5,-5..5.
Us aconsellem que feu altres proves que us permetran copsar
millor els detalls explicats, qu eno es veuen prou bé en els gràfics
anteriors els quals, per raons didàctiques hem volgut mostrar un
al costat de l'altre.
L'estructura sintàctica de la comanda dibuixa3d
és anàloga a la de la comanda dibuixa, que ja coneixeu i
els atributs de dibuix correpsonents a la comanda dibuixa
sòn vàlids també en aquest cas, però naturalment
hi ha altres possibilitats, algunes de les quals comentem tot seguit.
Ara bé, us aconsellem que les consulteu al manual, al capítol
de Gràfics3d de la Guia ràpida o a l'entrada
opcions dibuixa3d de l'índex alfabètic.
És interessant combinar-les amb les opcions de tauler que s'apliquen
a tot el dibuix i no a una figura (per exemple fer un gràfic sense
els eixos ni el cub referencial)
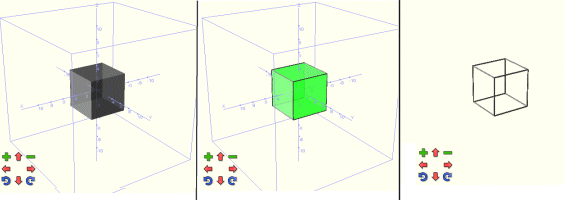
Tres representacions del mateix cub fetes amb
les comandes que s'indiquen seguidament:

És interessant que observeu:
- El fet que, per defecte, les figures estan representades amb uns efectes
d'acoloriment i transparència que donen idea "de què
queda davant i què queda al darrere" sense que es vegin
de manera específica les arestes.
- La possibilitat de dibuixar les arestes (amb l'opció filferro=cert),
de canviar el color del gràfic i de visualitzar solament les
arestes (dient que no s'ompli la figura).
- La possibilitat d'eliminar els eixos i el cub de representació
(mostrar_cub=fals). En els gràfics 3D no hi ha la possibilitat
de mostrar l'engraellat (el que en diem lamalla).
 Sabeu
que en els gràfics 2D el fet de que es mostrin o no els eixos
o la malla es poden indicar directament passant un paràmetre
en una línia de comandes.Convé comentar que això
no és possible per als gràfics 3D, on les característiques
del tauler s'han de passar com a atributs en una comanda tauler. Sabeu
que en els gràfics 2D el fet de que es mostrin o no els eixos
o la malla es poden indicar directament passant un paràmetre
en una línia de comandes.Convé comentar que això
no és possible per als gràfics 3D, on les característiques
del tauler s'han de passar com a atributs en una comanda tauler.
|
| |
Per acabar farem una reflexió sobre el fet que, per a objectes
indefinits (plans, rectes, etc...) només es dibuixa "allò
que es veu en el cub de representació". Si bé, com
ja s'ha dit, ja estem molt acostumats a "retallar un gràfic
bidimensional" perquè e svegi només allò que
escau per la finestra de representació triada, això ja no
és tan intuïtiu a l'espai.
És ben habitual que el professorat que vol il·lustrar gràficament
un pla, amb un dibuix fet a mà a la pissarra, ho mostri així:

L'esquema anterior és ben intuïtiu però
no és estrictament un "dibuix 3D" perquè no hi
ha perspectiva ni elements referencials. Com veurem un pla quan la Wiris
ens l'ensenyi en perspectiva i només la zona inclosa en el cub
referencial? Pot mostrar-se d emaneres ben diferents. Vegeu-ne uns exemples:
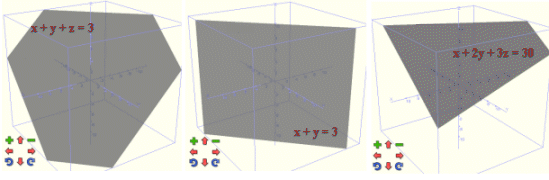
Tres aspectes que ens pot oferir la
representació d'un pla
Quan en el mòdul 5 treballem la geometria analítica de
l'espai n'haurem de tornar a parlar!!!
|
| |
A part de la geometria de les varietats lineals (que es comenta en una
pràctica del mòdul següent) la Wiris pot representar
cossos geomètrics, des d'un segment als políedres regulars,
passant per un gran nombre de figures. Per altra banda, amb les idees
que s'han comentat fins ara pel que fa als gràfics 3D segur que
ja us imagineu que cada figura que fem la podem motsrar des del punt de
vista que més ens inetressi, moure-la, dirar-la,...
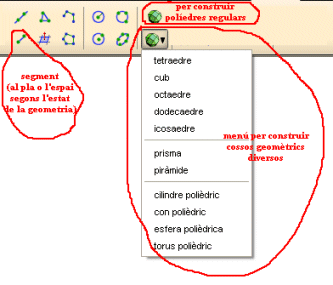
La definició d'aquests cossos es pot fer amb les icones corresponents
de la carpeta  ,
i amb un menu auxiliar. ,
i amb un menu auxiliar.
|
| |
Pel que fa als políedres regulars és clar que només
serviran com a argument els nombres de cares que poden donar un políedre
regular (4, 6, 8, 12, 20) i també veureu que les figures "amb
rodones" es mostren "poliedritzades": el primer argument
dela comanda es un nombre enter; com més gran sigui aquest nombre
enter, millor ens acostarem a la figura que volem (però, alerta,
pot haver-hi problemes de memòria!). Naturalment la consulta al
manual de la Wiris (o la investigació a base de prova i error que
tant ens agrada!) completarà aquesta breu introducció si
voleu conèixer els detalls sintàctics de cada comanda.
Vegeu tot seguit, per acabar la pràctica,
una pantalla activa amb alguns exemples. Observareu que s'ha seguit la
manera recomanada de procedir habitualment: primer es defineix el cos
o cossos que volem dibuixar i posteriorment es dibuixen (amb dibuixa3d
o bé amb dibuixa si abans hem establert
l'estat de la geometria com 3D.)
|