| |
L'objectiu d'aquesta pràctica és arribar a
controlar el funcionament de les ordres que permeten moure objectes en
l'espai tridimensional.
|
| |
|
| |
Ordres: Alinear, Simetría 3D, Gira
3D, Matriz 3D |
| |
|
|
|
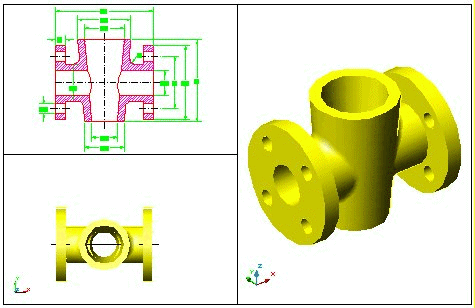
La pràctica consisteix en la creació d'un
sòlid per a la unió de dos sòlids de revolució
i altres sòlids per crear per diferència els buits necessaris.
Es disposa d'un fitxer de suport, en el qual hi ha els blocs per fer les
figures de revolució.
|
| |
|
| |
Figura 1. Làmina finalitzada
|
| |
|
| |
1. Preparació del document |
| |
|
|
|
El dibuix representa 2 eixos perpendiculars amb un punt sobre un d'ells
per inserir els blocs predefinits.
- Activeu la barra d'eines Ventanas gráficas.
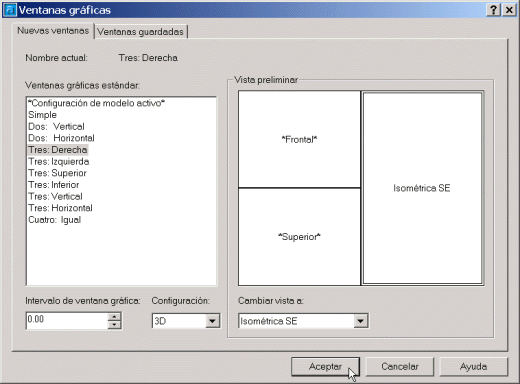
- Amb la primera icona de l'esquerra accedireu al quadre de selecció
de finestres gràfiques. Feu les seleccions de la imatge.
|
| |
| |
Figura 2. Selecció de la configuració
de Ventanas
|
| |
- També s'hi pot arribar des del menú Ver
| Ventanas gráficas | Ventanas guardadas.
Seleccioneu l'opció Configuración
3D.
- Insertar
 el bloc de nom, Secció cònica,
en el punt marcat sobre l'eix horitzontal. (Factors d'escala: 1,1 i
1, rotació = 0.)
el bloc de nom, Secció cònica,
en el punt marcat sobre l'eix horitzontal. (Factors d'escala: 1,1 i
1, rotació = 0.)
- Descomponer
 el bloc. Es converteix en una regió. Per comprovar-ho, accediu
a l'ordre Propiedades i veureu com
a la casella superior es diu que es tracta d'una
Región.
el bloc. Es converteix en una regió. Per comprovar-ho, accediu
a l'ordre Propiedades i veureu com
a la casella superior es diu que es tracta d'una
Región.
|
|
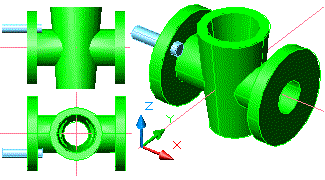
Figura 3. El bloc inserit. Vista en
planta i en finestra Isom. SE
|
|
|
Els blocs no es poden utilitzar directament com a contorns per generar
sòlids. S'han de descompondre prèviament.
El treball descrit a partir d'ara es pot fer en qualsevol finestra gràfica.
S'està i se seguirà treballant únicament en el sistema
de coordenades universals. D'aquesta manera, el programa ens obliga
a utilitzar els comandaments 3D, per orientar i recol·locar els
objectes en l'espai.
|
| |
|
| |
2. Creació del sòlid |
| |
|
|

|
-
Feu actual la Capa
Sòlid 1.
-
Amb l'ordre Revolución
seleccioneu la regió del pas anterior
i apliqueu-hi una revolució de 360º entorn a l'eix vertical.
Comando: _revolve
Densidad de estructura alámbrica actual: ISOLINES=4
Designe objetos: Assenyaleu la regió.
1 encontrados
Designe objetos: Retorn per
acabar la designació.
Precise punto inicial de eje de revolución o
defina eje mediante [Objeto/Abscisas/oRdenadas]:.
Indiqueu el punt superior de l'eix vertical
Precise punto final de eje: Indiqueu el punt
inferior de l'eix vertical
Precise ángulo de revolución <360>: Retorn.
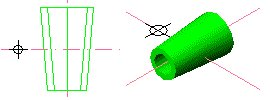
|
| |
Figura 4. La regió ja revolucionada
|
| |
- Insertar
 el bloc de nom Secció tubular en el mateix punt d'abans,
sobre l'eix horitzontal. (Factors d'escala: 1,1 i 1, rotació
= 0.)
el bloc de nom Secció tubular en el mateix punt d'abans,
sobre l'eix horitzontal. (Factors d'escala: 1,1 i 1, rotació
= 0.)
- Descomponer
 el bloc. Es converteix en regió.
el bloc. Es converteix en regió.
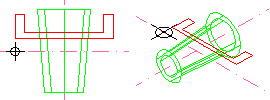
|
| |
Figura 5. Inserció del segon
bloc
|
|
|
-
Feu actual la Capa
Sòlid 2.
-
Amb l'ordre Revolución
seleccioneu la nova regió del pas
anterior i apliqueu-hi una revolució de 360º entorn a
l'eix horitzontal.
Comando: _revolve
Densidad de estructura alámbrica actual: ISOLINES=4
Designe objetos: Assenyaleu la regió.
1 encontrados
Designe objetos: Retorn per
acabar la designació.
Precise punto inicial de eje de revolución o
defina eje mediante [Objeto/Abscisas/oRdenadas]: Indiqueu
el punt esquerre de l'eix horitzontal
Precise punto final de eje: Indiqueu el punt
dret de l'eix horitzontal.
Precise ángulo de revolución <360>: Retorn.
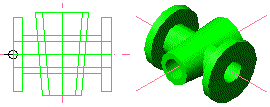
|
|
|
Figura 6. Revolució de la segona secció
inserida
|
|
|
Ara es farà la Unión dels
dos sòlids.
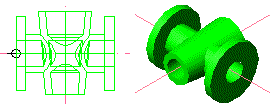
|
| |
Figura 7. Els dos sòlids units
|
| |
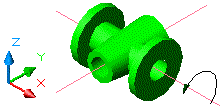
Ara s'aixecarà el sòlid resultant, ja que aquest està
tombat, sobre el plànol horitzontal. Per fer-ho s'utilitza l'ordre
Girar 3D. L'eix de rotació en
aquest cas és X.
|
| |
Figura 8. Rotació 3D entorn a l'eix X,
aplicable al sòlid
|
| |
|
| |
3. Gira 3D |
| |
|
|
|
Ordre: Girar 3D.
Menú: Modificar |
Operación en 3D | Girar 3D
Comando: _rotate3d
Inicializando...
Ángulo positivo actual: ANGDIR=contrario al sentido horario ANGBASE=0
Designe objetos:
Cliqueu sobre el sòlid. 1 encontrados
Designe objetos: Retorn
per acabar la designació.
Precise primer punto del eje o defínalo
mediante
[Objeto/úLTimo/Vista/ejeX/ejeY/ejeZ/2puntos]: X
es pot indicar sobre el menú
contextual.
Precise un punto del eje X <0,0,0>: Indicar
un punt qualsevol de l'eix X del sòlid.
Precise ángulo de rotación o [Referencia]: 90
|
| |
Figura 9. El sòlid després de fer la rotació
3D
|
|
|
Per definir l'eix de rotació, l'AutoCAD
dóna diverses opcions. En aquest cas, s'ha escollit l'eje
X, i després el programa demana un punt de pas de l'eix,
ja que hi ha infinits vectors o eixos paral·lels a l'orientació
de l'eix X de l'SCP actiu.
En el cas d'haver seleccionat dos puntos,
únicament s'haurien indicat dos punts de l'eix (paral·lel
a X) que passa per la peça. Segons la direcció
que determinen els dos punts indicats, s'està definint un vector
(que mira a dreta o a esquerra), i això implica que l'angle de
rotació indicat pot resultar en sentit horari o trigonomètric.
La diferència entre la rotació 2D i la 3D és que
amb la primera l'objecte es mourà dins del plànol actual
entorn a un punt de gir. En la rotació 3D l'objecte es mou en
l'espai, però en comptes d'indicar només un punt de gir,
s'ha d'indicar un vector definit per dos punts.
|
|
|
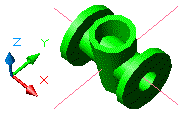
En el sòlid, vist des d'un altre angle, s'aprecia que està
travessat pel cos cilíndric, del qual era segon sòlid, i
d'altra banda, el forat del cos cilíndric queda travessat per la
zona cònica. S'ha de buidar tot això.
Per foradar o treure el tros cilíndric que passa dins del con:
- S'ha de crear un sòlid de forma cònica que coincideixi
amb la forma interior del con.
Per foradar o treure el tros cònic que hi ha a l'interior del
cilindre:
- S'ha de crear un cilindre que travessi horitzontalment el sòlid
pel seu eix X, actual.
|
| |
| |
Figura 10. El sòlid vist des d'un altre angle
|
|
|
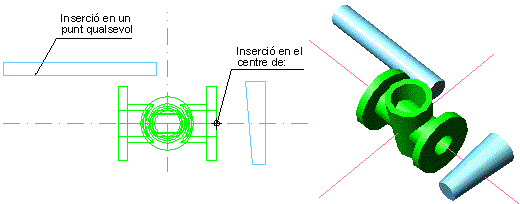
Les insercions d'ara es faran preferiblement en la finestra gràfica
de la planta.
- Feu actual la Capa Buits.
- Ordre Insertar
 el bloc Buit-cònic. S'insereix en el centre del forat
de la part cilíndrica. Es podria utilitzar un altre punt qualsevol.
el bloc Buit-cònic. S'insereix en el centre del forat
de la part cilíndrica. Es podria utilitzar un altre punt qualsevol.
- Ordre Insertar
 el bloc Buit-cilíndric. S'insereix en un punt qualsevol.
el bloc Buit-cilíndric. S'insereix en un punt qualsevol.
- Descomponer
 els blocs. Es converteixen en regions.
els blocs. Es converteixen en regions.
|
| |
|
|
- Ordre: Revolución
 . .
- Seleccioneu la regió Buit Cònic
i feu-hi una revolució de 360º entorn al seu eix vertical.
(Línia vertical de la dreta.)
- Seleccioneu la regió Buit Cilindric
i feu-hi una revolució de 360º entorn al seu eix horitzontal.
(La seva horitzontal de sota.)
|
| |
| |
Figura 11. Inserció dels blocs que perforen el
sòlid, en planta i vista 3D
|
| |
|
| |
4. Alinear |
| |
|
|
|
Ara s'ha d'aplicar l'ordre Alinear. Primer
es col·loca el buit-cònic dins de la part cònica
del sòlid verd. El seu funcionament és el següent:
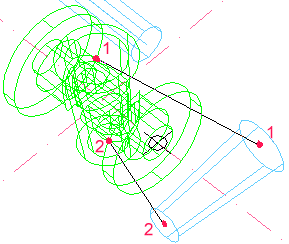
- L'AutoCAD demana un primer punt d'origen
i després el primer punt de destí. S'indica com a punt
d'origen el centre de la base gran del con blau, i com a punt de destí
el punt centre superior del con verd de la peça.
- A continuació, es demana un segon punt d'origen i un segon
punt de destí. S'indica com a punt d'origen el centre de la base
petita del con blau, i com a punt de destí el punt centre inferior
del con verd de la peça.
|
| |
|
|
- Ordre: Alinear. Menú: Modificar
| Operación en 3D | Alinear.
Comando: _align
Inicializando...
Designe objetos: Cliqueu sobre el con
blau. 1 encontrados
Designe objetos: Retorn per
acabar la designació.
Precise el primer punto de origen: Indiqueu
el centre de la base gran del con blau (punt
1).
Precise el primer punto de mira: Assenyaleu
el punt centre superior del con verd
(punt 1).
Precise el segundo punto de origen: El centre
de la base petita del con blau (punt
2).
Precise el segundo punto de mira: El punt
centre inferior del con verd (punt
2).
Precise el tercer punto de origen o <continuar>: Retorn.
(En aquest cas, no és necesari indicar una tercera parella de
punts.)
¿Desea atribuir una escala a los objetos según
los puntos de alineación?
[Sí/No] <N>: Retorn.
|
| |
| |
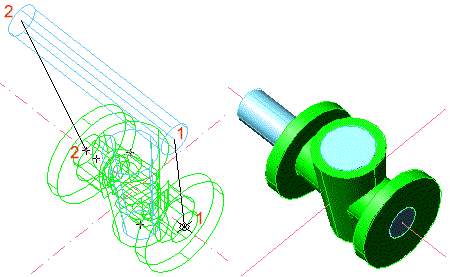
Figura 12. Punts definidors de l'ordre Alinear
|
|
|
Ara s'ha de fer l'alineació del cilindre blau, amb l'eix horitzontal
del sòlid verd.
- Ordre: Alinear.
Comando: _align
Designe objetos: Cliqueu sobre el cilindre
blau 1 encontrados
Designe objetos: Retorn per
acabar la designació.
Precise el primer punto de origen:Indiqueu
el centre 1 del cilindre blau.
Precise el primer punto de mira: Assenyaleu
el centre 1 de la peça verd.
Precise el segundo punto de origen:Indiqueu
el centre 2 del cilindre blau.
Precise el segundo punto de mira: Assenyaleu
el centre 2 de la peça verd.
Precise el tercer punto de origen o <continuar>:
Retorn.
¿Desea atribuir una escala a los objetos según
los puntos de alineación?
[Sí/No] <N>: Retorn.
|
| |
| |
Figura 13. Alineament del cilindre blau
|
|
|
- Ordre: Diferencia
 . .
- Assenyalar el sòlid verd com a positiu, i els dos sòlids
blaus com a negatius o sólidos a sustraer.
- Amb l'ordre Orbita
 ,
busqueu un angle de visió com el de sota per comprovar els buidatges. ,
busqueu un angle de visió com el de sota per comprovar els buidatges.

|
| |
| |
Figura 13. Resultat després de diferenciar els
sòlids
|
|
|
Falten els forats per a la subjeció de la peça en els seus
extrems. Per fer-ho, es crea un cilindre sòlid, de 10 unitats de
diàmetre i altura 40 . Es continua estant en el sistema
de coordenades universals.
- Ordre:
 Cilindro Cilindro
Comando: _cylinder
Densidad de estructura alámbrica actual: ISOLINES=4
Precise centro de base de cilíndro o [Elíptico] <0,0,0>:
Qualsevol punt en la imatge a l'esquerra del
sòlid verd.
Precise radio para base de cilíndro o [Diámetro]: 5
Precise altura de cilindro o [Centro del otro extremo]:
40

|
| |
| |
Figura 14. Dibuix d'un cilindre sòlid
en un punt qualsevol
|
| |
Comando: _align
Inicializando...
Designe objetos: Cliqueu sobre el
cilindre blau. 1 encontrados
Designe objetos:
Retorn per acabar la designació.
Precise el primer punto de origen: _qua
de quadrant punt 1 del cilindre.
Precise el primer punto de mira: _qua de
quadrant punt 1 del sòlid verd.
Precise el segundo punto de origen: _qua
de quadrant punt 2 del cilindre.
Precise el segundo punto de mira: _qua de
quadrant punt 2 del sòlid verd.
Precise el tercer punto de origen o <continuar>: _cen
de centre de la base del cilindre.
recise el tercer punto de mira: _nea a
Cercano a l'eix horitzontal per l'esquerra.
|
| |
Figura 15. Alineació del cilindre en el sòlid
verd
|
|
|
Ara es desplaça aquest cilindre de
manera que travessi el sòlid verd. El desplaçament es
fa des d'un punt qualsevol de l'espai, 15 unitats en direcció
X positiva, 0 unitats en direcció
Y, i -5 unitats en direcció
Z negativa.
Comando: _move
Designe objetos: Cliqueu sobre el cilindre
1 encontrados
Designe objetos: Retorn per acabar.
Precise punto base o de desplazamiento: <Refent act> Qualsevol
punt, per exemple el centre d'una base del cilindre.
Precise segundo punto del
desplazamiento o <usar primer punto como desplazamiento>: @15,0,-5
|
| |
Figura 16. Desplaçament del cilindre
|
|
|
El cilindre s'ha de girar 45º en torn a l'eix X
de la figura, de manera que quedi en la posició correcta segons
es pot veure en la figura 1.
Designe objetos: Assenyaleu
el cilindre blau. 1 encontrados
Designe objetos: Retorn
per acabar la designació.
Precise primer punto
del eje o defínalo mediante
[Objeto/úLTimo/Vista/ejeX/ejeY/ejeZ/2puntos]: X.
Escolliu l'eix X del menú contextual.
Precise un punto del eje X <0,0,0>: _nea
a Assenyaleu qualsevol punt de l'eix
X del sòlid verd.
Precise ángulo de rotación o [Referencia]: 45
|
| |
Figura 16. Rotació 3D del cilindre entorn a l'eix
X del sòlid
|
| |
|
| |
5. Matriz 3D |
| |
|
|
|
Mitjançant l'ordre Matriz
3D, polar, es copia el cilindre
blau 4 vegades entorn de l'eix X de la
peça. Les matrius 3D requereixen un eix per aplicar-les, en comptes
del punt que requereixen les matrius 2D.
Comando: _3darray
Inicializando... 3DARRAY cargada.
Designe objetos: Cliqueu sobre el cilindre
blau. 1 encontrados
Designe objetos: Retorn per
acabar la designació.
Indique el tipo de matriz [Rectangular/Polar] <R>:
P
Indique el número de elementos de la matriz: 4
Precise el ángulo a rellenar (+=trigon., -=horario)
<360>: Retorn.
¿Girar objetos de matriz? [Sí/No] <S>:
S
Precise centro de matriz: _nea
a Indiqueu un punt de l'eix X
del sòlid.
Precise segundo punto del eje de rotación: _nea
a Indiqueu un altre punt de l'eix X del sòlid.
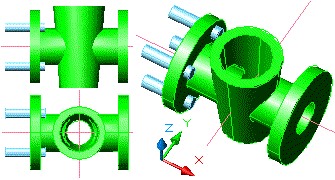
|
| |
Figura 17. Aplicació de la Matriz 3D polar
|
| |
|
| |
6. Simetría 3D |
| |
|
|
|
S'han de copiar per Simetría
3D els 4 cilindres blaus al costat de la dreta.
La Simetría
3D utilitza un plànol definit per 3 punts, per fer la
reflexió.
En aquest cas, el plànol ques s'utilitza
és paral·lel al YZ i
passa pel centre del sòlid. Aquest punt de pas pot ser el centre
o un quadrant de la part cònica del sòlid verd, com també
qualsevol punt de l'eix vermell paral·lel a Y que passa
pel sòlid.
|
| |
|
|
- Ordre: Simetria
3D. Menú: Modificar
| Operación en 3D | Simetria 3D
Comando: _mirror3d
Designe objetos: Seleccioneu un a un els 4
cilindres blaus. 4 total
Designe objetos: Retorn per
acabar la designació.
Precise primer punto del plano de simetría
(3 puntos) o
[Objeto/úLTimo/ejeZ/Vista/XY/YZ/ZX/3puntos] <3puntos>:
YZ
Precise punto en el plano YZ <0,0,0>: Assenyaleu
qualsevol punt de l'eix Y que passa pel centre del sòlid.
¿Borrar objetos originales? [Sí/No] <N>:
N
|
| |
| |
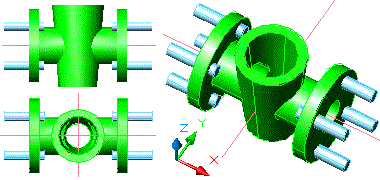
Figura 18. Resultat d'aplicar la Simetría
3D respecte al plànol YZ
|
|
|
Apliqueu ara la diferència de sòlids per obtenir el forats
de la peça.
- Ordre: Diferencia
 . .
- Indiqueu primer el sòlid verd com a positiu, i després
els 8 cilindres com a Objetos a sustraer.
|
| |
| |
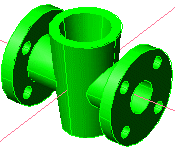
Figura 18. Els 8 forats cilíndrics fets
|
|
|
Per acabar la pràctica només cal arrodonir amb radi 6 unitats
la intersecció de les parts cilíndrica i cònica.
S'emprarà l'odre Empalme.
Comando: _fillet
Parámetros actuales: Modo = Recortar, Radio = 10.0000
Designe el primer objeto o [Polilínea/RAdio/Recortar]: RA
Precise radio de empalme <10.0000>: 6
Designe el primer objeto o [Polilínea/RAdio/Recortar]:
Indiqueu una de les arestes d'intersecció.
Indique radio de empalme <6.0000>: Retorn.
Designe una arista o [Cadena/Radio]:Indiqueu
l'altra de les arestes d'intersecció.
Designe una arista o [Cadena/Radio]: Retorn.
2 arista(s) seleccionadas para empalme.
|
| |
| |
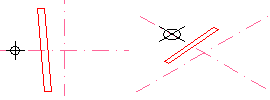
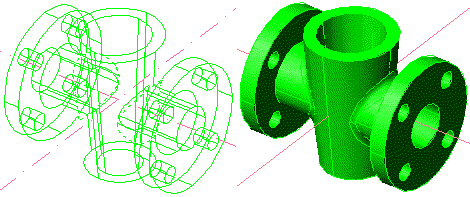
Figura 18. A l'esquerra, selecció d'arestes (a
traços) a Empalmar, i a dreta el resultat
|
| |
|
|
|
Deseu el dibuix a la carpeta Practiques
amb el nom m7_pr1a.dwg. |
| |
|
 |
| |
|
| |
|