|
1. Girar tres variables
Feu un programa en el qual es faci servir la
funció: void
rota(int *a, int
*b, int *c)
Aquesta funció ha de girar
els valors de les variables enteres a, b, i c, és a dir:
el contingut de a passarà a b, el contingut de b
passarà a c i el contingut de c passarà a a. Per
exemple, si els valors de a, b i c abans de la
crida a la funció són:
a = 2
b = 3 c = 10
després de la crida haur ande ser:
a = 10
b = 2 c = 3
Evidentment, com que voleu
que la funció modifiqui els seus arguments, aquests han de ser punters.
Anomeneu l'arxiu
font m5e1.cpp.
|
|
2. Valor màxim d'un vector
Feu un programa en el qual es faci servir la funció: double
maxim(double * vector, int
grand)
Aquesta funció ha de tornar el màxim del
vector de nombres reals (vector) que té (grand)
elements del tipus double.
Anomeneu l'arxiu
font m5e2.cpp.
|
|
3. Cercar el Punt_Suma d'un vector de dimensió
M per N
S'anomena Punt_Suma d'un vector bidimensional
l'element que coincideix amb la suma de la resta d'elements del vector.
Per
exemple:
Donada
la matriu d'enters A de 3 per 4 (int A[3][4])
|
5 |
2 |
6 |
7 |
|
0 |
197 |
1 |
8 |
|
1 |
7 |
10 |
150 |
en la posició
[1][1], que conté l'enter 197, teniu el Punt_Suma que és el que
coincideix amb la suma de la resta de
cel·les (5
+ 2 + 6 + 7 + 0 + 1 + 8 + 1 + 7 + 10 + 150=197).
Escriviu un programa
que permeti recollir enters per emmagatzemar dins la matriu A de
M per N.
El programa treballa
utilitzant les directives #define per donar la grandària del
vector en temps de disseny. Més endavant veureu, amb l'assignació dinàmica
de memòria, com donar la mida del vector en temps d'execució:
#define M 3
#define N 4
Escriviu una funció amb el prototipus int Punt_Suma(int B[][N]);
que recollirà el vector i retornarà, si existeix, el Punt_Suma.
Anomeneu l'arxiu font m5e3.cpp.
|
|
4. Transposició d'una matriu nxm
Un dels problemes que es pot
plantejar després de fer la pràctica 7 és
què passa si la matriu no és quadrada. Això suposa un problema pel fet
que no es pot convertir una matriu de dimensió nxm en una matriu
de dimensió mxn. Una forma de resoldre aquest problema és fer
servir una única dimensió, és a dir, declarar la matriu com:
double
a[MAX_FILES*MAX_FILES];
Ara, si anomeneu n
al nombre de files i m al nombre de columnes, tot el codi és
semblant al de la pràctica canviant: a[i][j] per a[i*n+j],
i canviant n per m a la comprovació del segon bucle. Per
exemple, la part del codi que demana els elements de la matriu seria:
//introducció dels elements de A
for (i=0;i<n;i++){
for(j=0;j<m;j++){
printf("\na[%d,%d]=",i,j);
scanf("%lf",&a[i*m+j]);
}
}
|
També s'han de fer modificacions
a la funció transposada(a,n), afegint-hi un argument que correspongui
al nombre de columnes.
Anomeneu l'arxiu
font m5e4.cpp.
|
|
Exercicis
complementaris
Aquests exercicis serveixen per
completar aquest mòdul, però suposen una ampliació voluntària. No
és necessari entregar-los. No obstant això, és convenient fer-los
i lliurar-los.
5. Suavització d'un vector
Feu un programa que "suavitzi"
un vector introduït per l'usuari/ària. S'entén per suavitzar
substituir cada element per la mitjana aritmètica dels elements més
propers, és a dir:
uS[i]->(u[i-1]+u[i]+u[i+1])/3
si i diferent de 0 i n-1
uS[0]->(u[0]+u[1])/2 uS[n-1]=(u[n-2]+u[n-1])/2
Per exemple,
el vector u de la primera columna d'aquesta taula s'ha convertit
en el vector uS de la segona columna.
| u |
uS |
|
14 |
9,5 |
|
5 |
6,666666667 |
|
1 |
5,333333333 |
|
10 |
7,666666667 |
|
12 |
7,666666667 |
|
1 |
6,333333333 |
|
6 |
2,666666667 |
|
1 |
2,666666667 |
|
1 |
5,333333333 |
|
14 |
7,333333333 |
|
7 |
10,5 |
Per entendre bé el significat d'aquesta
suavització, veureu dos diagrames de barres corresponents als vectors
u i uS on es pot observar com en el segon vector
les diferències entre elements contigus són més petites:
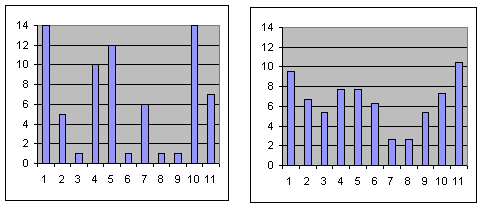
Anomeneu l'arxiu font m5e5.cpp.
6. La llei d'Hondt
Modifiqueu el programa de la pràctica
8 perquè el nombre d'escons i de partits es pugui entrar per teclat. Feu també
aquesta important modificació per perfeccionar el programa:
En el programa de la pràctica 8 hi ha un cas
que no s'ha tingut en compte, i és que quan s'avalua la funció nou_esc
per assignar un nou escó, en el cas que dos partits tinguin el mateix
valor de vots[]/(esc[]+1), l'escó s'hauria d'assignar al partit
més votat. Modifiqueu el que sigui necessari del programa de la pràctica
7 per considerar aquesta circumstància. Proveu-ho amb tres partits i
quatre escons, i que els vots dels tres partits siguin 40, 50 i 120.
Anomeneu l'arxiu
font m5e6.cpp.
(En el cas que els partits
que tenen el mateix valor de vots[]/(esc[]+1) tinguin també el mateix
nombre de vots (cosa molt poc probable), l'assignació es fa per sorteig
la primera vegada que hi hagi l'empat, i la resta de cops que es produeixi
l'empat s'assigna alternativament.)
|